| Codeforces Round 329 (Div. 2) |
|---|
| Закончено |
Учительница дала Антону большое домашнее задание по геометрии, но он как обычно его не сделал, поскольку участвовал в регулярном раунде Codeforces. В задание был дан набору из n прямых, определяемых уравнениями y = ki·x + bi. Требовалось определить, существует ли хотя бы одна точка пересечения двух прямых, лежащая строго внутри полосы ограниченной x1 < x2. Другими словами, правда ли что найдутся такие 1 ≤ i < j ≤ n и такие x', y', что:
- y' = ki * x' + bi, то есть точка (x', y') принадлежит прямой с номером i;
- y' = kj * x' + bj, то есть точка (x', y') принадлежит прямой с номером j;
- x1 < x' < x2, то есть точка (x', y') лежит внутри полосы ограниченной x1 < x2.
Вы же не оставите Антона в беде и поможете ему решить задание?
В первой строке входных данных находится целое число n (2 ≤ n ≤ 100 000) — количество прямых в задании. Во второй строке содержатся целые числа x1, x2 ( - 1 000 000 ≤ x1 < x2 ≤ 1 000 000) определяющие полосу, внутри которой требуется найти точку пересечения прямых.
В следующих n строках содержатся целые числа ki, bi ( - 1 000 000 ≤ ki, bi ≤ 1 000 000) — описание прямых. Гарантируется, что все прямые различны, то есть для любых двух i ≠ j верно, что либо ki ≠ kj, либо bi ≠ bj.
Выведите «Yes» (без кавычек), если существует хотя бы одно пересечение двух прямых, расположенное строго внутри полосы, иначе выведите «No» (без кавычек).
4
1 2
1 2
1 0
0 1
0 2
NO
2
1 3
1 0
-1 3
YES
2
1 3
1 0
0 2
YES
2
1 3
1 0
0 3
NO
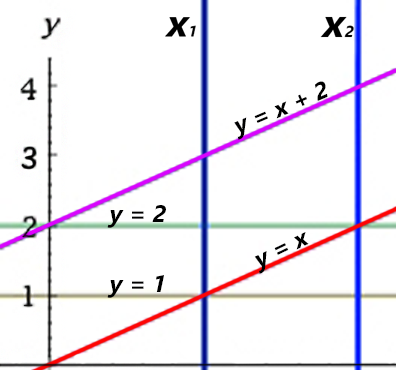
В первом примере прямые пересекаются только на границе полосы, но ни одного пересечения внутри нет.
| Название |
|---|




