C. Красивая функция
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Каждый день перед сном Руслан считал овец, но это ему не помогало. Теперь он нашёл себе занятие интереснее: он сначала загадывает какое-то множество окружностей на плоскости, а затем пытается определить какое-нибудь красивое множество точек, так чтобы внутри или на границе каждой загаданной окружности лежала хотя бы одна точка множества.

Вчера Руслан попробовал решить данную задачу, когда множество считается красивым, если оно определяется как (xt = f(t), yt = g(t)), для всех целых t от 0 до 50. При этом f(t) и g(t) должны быть корректными функциями.

Пусть w(t) и h(t) — корректный функции, а c — целое число от 0 до 50. Тогда функция s(t) является корректной, если она получена по одному из следующих правил:

  1. s(t) = abs(w(t)), где abs(x) означает взятие абсолютного значения числа x, то есть |x|;
  2. s(t) = (w(t) + h(t));
  3. s(t) = (w(t) - h(t));
  4. s(t) = (w(t) * h(t)), где  *  означает умножение, то есть (w(t)·h(t));
  5. s(t) = c;
  6. s(t) = t;

Вчера Руслан промучился всю ночь, но так и не справился с задачей. Теперь он просит вас написать программу, вычисляющую подходящие f(t) и g(t) для любого набора из не более чем 50 окружностей.

В каждой из функций f(t) и g(t) должно быть использовано не более 50 операций умножения. Длина функции не должна превышать 100·n символов. В функции не должно быть пробелов.

Руслан плохо работает с большими числами, поэтому функции f(t) и g(t) должны быть выбраными такими, чтобы для всех t от 0 до 50 все промежуточные вычисления и итоговое значение по абсолютному значению не превосходили 109.

Входные данные

В первой строке входных данных записано число n (1 ≤ n ≤ 50) — количество окружностей, загаданных Русланом. Следующие n строк содержат по три целых числа xi, yi, ri (0 ≤ xi, yi ≤ 50, 2 ≤ ri ≤ 50) — координаты и радиус i-й окружности.

Выходные данные

В первой строке выведите корректную функцию f(t). Во второй строке вывести корректную функцию g(t). Множество точек (xt = f(t), yt = g(t)) (0 ≤ t ≤ 50) должно удовлетворять условию, что для любой из n окружностей найдётся точка из данного мноежства лежащая внутри ли на границе.

Примеры
Входные данные
3
0 10 4
10 0 4
20 10 4
Выходные данные
t 
abs((t-10))
Примечание

Корректные функции:

  1. 10
  2. (1+2)
  3. ((t-3)+(t*4))
  4. abs((t-10))
  5. (abs((((23-t)*(t*t))+((45+12)*(t*t))))*((5*t)+((12*t)-13)))
  6. abs((t-(abs((t*31))+14))))

Некорректные функции:

  1. 3+5+7 (не хватает скобок, должно быть ((3+5)+7) или (3+(5+7)))
  2. abs(t-3) (не хватает скобок, должно быть abs((t-3))
  3. 2+(2-3 (лишняя скобка)
  4. 1(t+5) (нет арифметической операции между 1 и скобкой)
  5. 5000*5000 (число превышает максимальное)
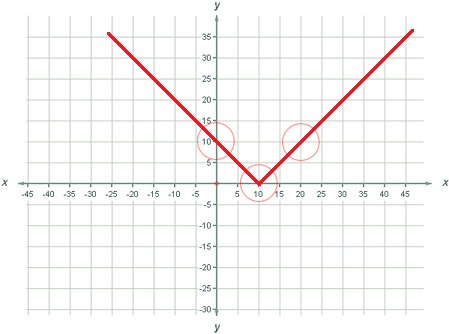На картинке показано одно из возможных решений. Например, при t = 0;10;20 полученные координаты принадлежат заданным окружностям.