| Codeforces Round 329 (Div. 2) |
|---|
| Закончено |
У Богдана сегодня День Рождения и мама подарила ему дерево, состоящее из n вершин. На ребре i было написано число xi. Напомним, что деревом называется связный неориентированный граф без циклов. После этого на вечеринку к Богдану последовательно приходят m гостей. Когда приходит i-й гость, он делает ровно одну из двух операций:
- Выбирает некоторое число yi, а так же две вершины ai и bi. После этого двигаясь по рёбрам дерева проходит от вершины ai до вершины bi кратчайшим путём (такой путь в дереве, конечно, единственный). Каждый раз проходясь по какому-то ребру j, он заменяет своё текущее число yi на
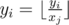 , то есть на целую часть деления yi на xj.
, то есть на целую часть деления yi на xj. - Выбирает некоторое ребро pi, и заменяет написанное на нём значение xpi на целое положительное число ci < xpi.
Богдан заботится о своих гостях и решил автоматизировать данный процесс. Напишите программу, которая проделает все применяемые гостями операции, и каждому гостю выбравшему операцию первого типа сообщит результирующее значение yi.
В первой строке входных данных содержатся два числа n и m (2 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000) — количество вершин в дереве, подаренном Богдану, и количесвто гостей на вечеринке соответственно. В следующей n - 1 строке содержится описание рёбер, i-я из этих строк содержит три целых числа ui, vi, xi (1 ≤ ui, vi ≤ n, ui ≠ vi, 1 ≤ xi ≤ 1018), обозначающих ребро между вершинами ui и vi, на котором написано число xi. Далее следуют m строк, которые описывают гостей Богдана. Каждое описание содержит три или четыре целых числа и имеет вид:
- 1 ai bi yi — соответствует гостям, выбравшим операцию первого типа.
- 2 pi ci — соответствует гостям, выбравшим операцию второго типа.
Для каждого гостя, выбравшего операцию первого типа, выведите результирующее значение для выбранного им yi.
6 6
1 2 1
1 3 7
1 4 4
2 5 5
2 6 2
1 4 6 17
2 3 2
1 4 6 17
1 5 5 20
2 4 1
1 5 1 3
2
4
20
3
5 4
1 2 7
1 3 3
3 4 2
3 5 5
1 4 2 100
1 5 4 1
2 2 2
1 1 3 4
2
0
2
Изначально дерево выглядит так:
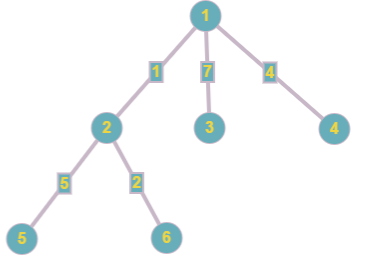
На первый запрос ответом будет 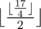 = 2
= 2
После изменения третьего ребра дерево выглядит так:
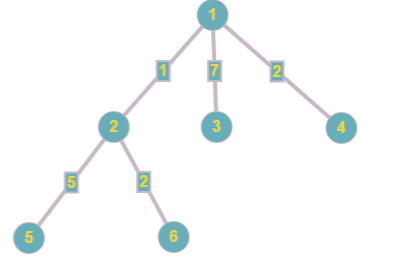
На второй запрос ответом будет 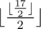 = 4
= 4
В третьем запросе начальная и конечная вершина совпадает, то есть ответом будет исходное число 20.
После изменения четвертого ребра дерево выглядит так:
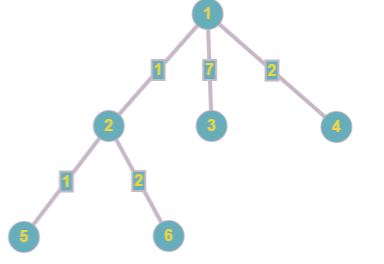
В последнем запросе ответом будет 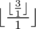 = 3
= 3
| Название |
|---|




