| Codeforces Round 333 (Div. 1) |
|---|
| Закончено |
Функция 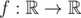 называется Липшицевой, если найдётся такое действительное число K, что неравенство |f(x) - f(y)| ≤ K·|x - y| выполняется для всех
называется Липшицевой, если найдётся такое действительное число K, что неравенство |f(x) - f(y)| ≤ K·|x - y| выполняется для всех 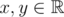 . Мы будем иметь дело с более... дискретным вариантом этого термина.
. Мы будем иметь дело с более... дискретным вариантом этого термина.
Для массива 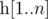 определим его константу Липшица
определим его константу Липшица 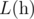 следующим образом:
следующим образом:
- если n < 2,
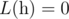
- если n ≥ 2,
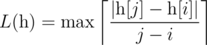 по всем 1 ≤ i < j ≤ n
по всем 1 ≤ i < j ≤ n
Другими словами, 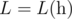 — это наименьшее неотрицательное целое число, такое, что |h[i] - h[j]| ≤ L·|i - j| выполняется для всех 1 ≤ i, j ≤ n.
— это наименьшее неотрицательное целое число, такое, что |h[i] - h[j]| ≤ L·|i - j| выполняется для всех 1 ≤ i, j ≤ n.
Вам дан массив  размера n и q запросов вида [l, r]. Для каждого запроса рассмотрим подмассив
размера n и q запросов вида [l, r]. Для каждого запроса рассмотрим подмассив 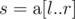 ; определите сумму констант Липшица всех подмассивов
; определите сумму констант Липшица всех подмассивов  .
.
В первой строке входных данных записано два числ n и q (2 ≤ n ≤ 100 000, 1 ≤ q ≤ 100) — длина массива  и количество запросов соответственно.
и количество запросов соответственно.
Во второй строке записано n целых чисел 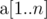 (
(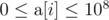 ).
).
Следующие q строк описывают запросы, i-я из них содержит два числа li и ri (1 ≤ li < ri ≤ n).
Выведите ответы на все запросы в том порядке, в котором они даны во входных данных. Для i-го запроса выведите единственное целое число — сумму констант Липшица всех подмассивов 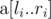 .
.
10 4
1 5 2 9 1 3 4 2 1 7
2 4
3 8
7 10
1 9
17
82
23
210
7 6
5 7 7 4 6 6 2
1 2
2 3
2 6
1 7
4 7
3 5
2
0
22
59
16
8
В первом запросе первого примера константы Липшица подмассивов 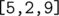 длиной не менее 2 таковы:
длиной не менее 2 таковы:
Ответом на запрос является их сумма.
| Название |
|---|