| Codeforces Round 333 (Div. 1) |
|---|
| Закончено |
В городе, где живет Клеофас, есть известный музей. В этом музее уже давно выставлено n экспонатов (пронумерованных от 1 до n); i-й экспонат имеет ценность vi и массу wi.
Недавно музей купила большая финансовая группа и начала менять набор экспонатов. Примерно в то же время Клеофас... скажем так, заинтересовался этим музеем.
Вам следует обработать q событий трёх типов:
- тип 1 — музей выставляет экспонат ценностью v и массой w; экспонат, появляющийся в i-м событии этого типа, получает номер n + i (смотрите пояснения к примерам);
- тип 2 — музей убирает экспонат номер x и аккуратно относит его в хранилище;
- тип 3 — Клеофас заходит в музей и задаётся вопросом (конечно, без какой-либо конкретной причины): если будет ограбление и украдут экспонаты с общей массой не более m, то какова может быть их максимальная суммарная ценность?
Пусть для каждого события типа 3 s(m) является максимально возможной общей ценностью украденных экспонатов с общей массой ≤ m.
Формально, пусть D — множество номеров всех экспонатов, на данный момент выставленных напоказ (таким образом, изначально D = {1, ..., n}). Пусть P(D) будет множеством всех подмножеств D и пусть
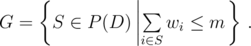
Тогда s(m) определяется как
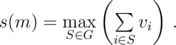
Вычислите s(m) для каждого 
. Обратите внимание на специальный формат выходных данных.
В первой строке входных данных записаны два целых числа n и k (1 ≤ n ≤ 5000, 1 ≤ k ≤ 1000) — изначальное количество экспонатов в музее и максимальная интересная суммарная масса экспонатов.
Затем следуют n строк, i-я из которых содержит два положительных целых числа vi и wi (1 ≤ vi ≤ 1 000 000, 1 ≤ wi ≤ 1000) — ценность и масса i-го экспоната соответственно.
В следующей строке записано единственное целое число q (1 ≤ q ≤ 30 000) — количество событий.
В каждой из следующих q строк записано описание одного события в следующем формате:
- 1 v w — событие типа 1, добавляется новый экспонат с ценностью v и массой w (1 ≤ v ≤ 1 000 000, 1 ≤ w ≤ 1000);
- 2 x — событие типа 2, экспонат с номером x убирается в хранилище; гарантируется, что убираемый экспонат выставлялся в этот момент;
- 3 — событие типа 3, Клеофас заходит в музей и задается своим странным вопросом.
Гарантируется, что в одном тесте будет не более 10 000 событий типа 1 и хотя бы одно событие типа 3.
Так как количество значений s(m) может оказаться большим, выведите ответы на события типа 3 в особом формате.
Для каждого события типа 3 рассмотрим значения s(m), рассчитанные для вопроса Клеофаса, которым он задался в некоторый момент времени; выведите единственное число
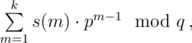
где p = 107 + 19 и q = 109 + 7.
Выводите ответы на события типа 3 в том порядке, в котором они упоминаются во входных данных.
3 10
30 4
60 6
5 1
9
3
1 42 5
1 20 3
3
2 2
2 4
3
1 40 6
3
556674384
168191145
947033915
181541912
3 1000
100 42
100 47
400 15
4
2 2
2 1
2 3
3
0
В первом примере количество выставленных экспонатов и значения s(1), ..., s(10) для отдельных событий типа 3 таковы, по порядку:
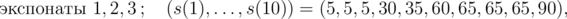
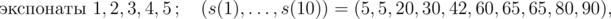
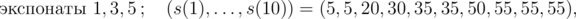
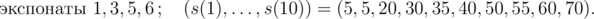
Ценности отдельных экспонатов таковы: v1 = 30, v2 = 60, v3 = 5, v4 = 42, v5 = 20, v6 = 40 и их массы таковы: w1 = 4, w2 = 6, w3 = 1, w4 = 5, w5 = 3, w6 = 6.
Во втором примере единственный вопрос задается после того, как все экспонаты уже убраны, так что s(m) = 0 для любых m.
