| Codeforces Round 344 (Div. 2) |
|---|
| Закончено |
Блейк управляет крупной компанией «Blake Technologies». Он очень любит свою компанию и считает, что она должна быть самой лучшей, по этой причине каждый кандидат, который хочет в ней работать, должен пройти собеседование. Оно состоит всего из одной интересной задачи, которую нужно решить.
Определим функцию f(x, l, r) как побитовое «ИЛИ» (будем обозначать как OR) чисел xl, xl + 1, ..., xr, где xi — элемент массива x с индексом i. Вам даны два массива a и b длины n. Нужно определить максимальное значение f(a, l, r) + f(b, l, r) по всем 1 ≤ l ≤ r ≤ n.
В первой строке входных данных записано одно целое число n (1 ≤ n ≤ 1000) — длина массивов a и b.
Во второй строке записаны n целых чисел ai (0 ≤ ai ≤ 109).
В третьей строке записаны n целых чисел bi (0 ≤ bi ≤ 109).
Выведите единственное целое число — максимальное значение f(a, l, r) + f(b, l, r) по всем 1 ≤ l ≤ r ≤ n.
5
1 2 4 3 2
2 3 3 12 1
22
10
13 2 7 11 8 4 9 8 5 1
5 7 18 9 2 3 0 11 8 6
46
Напомним, что значением побитового «ИЛИ» двух неотрицательных целых чисел a и b называется такое число c = a OR b, у которого в каждом разряде в двоичной записи стоит единица, если и только если хотя бы у одного из двух чисел a или b стоит единица в соответствующем разряде в двоичной записи.
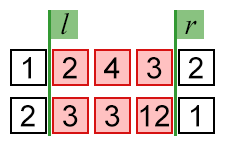
В первом примере максимальный ответ получается при l = 2 и r = 4, так как f(a, 2, 4) + f(b, 2, 4) = (2 OR 4 OR 3) + (3 OR 3 OR 12) = 7 + 15 = 22. Максимальный ответ можно получить и другими способами, например при l = 1 и r = 4, l = 1 и r = 5, l = 2 и r = 4, l = 2 и r = 5, l = 3 и r = 4 или при l = 3 и r = 5.
Во втором примере максимальный ответ получается при l = 1 и r = 9.
| Название |
|---|




