| VK Cup 2016 - Раунд 1 |
|---|
| Закончено |
У полярного медвежонка Лимака мало игрушек, поэтому он постоянно играет с многочленами (полиномами).
Он считает многочлен правильным, если тот имеет степень n и все его коэффициенты являются целыми числами не превосходящими k по абсолютному значению. Формально, пусть a0, a1, ..., an это коэффициенты многочлена 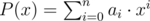 . Тогда многочлен P(x) является правильным если выполнены следующие условия:
. Тогда многочлен P(x) является правильным если выполнены следующие условия:
- ai является целым числом для всех i от 0 до n;
- |ai| ≤ k для всех i от 0 до n;
- an ≠ 0.
Лимаку недавно подарили правильный многочлен P с коэффициентами a0, a1, a2, ..., an. Он обратил внимание, что P(2) ≠ 0 и теперь хочет это исправить. Лимак хочет изменить ровно один коэффициент многочлена P, так чтобы получить правильный многочлен Q степени n, такой что Q(2) = 0. Вычислите, сколькими способами он может это сделать. Два способа следует считать различными, если коэффициенты полученных многочленов различаются.
В первой строке входных данных записаны целые числа n и k (1 ≤ n ≤ 200 000, 1 ≤ k ≤ 109) — степень многочлена и ограничение на абсолютное значение его коэффициентов.
Во втором строке записано n + 1 целое число a0, a1, ..., an (|ai| ≤ k, an ≠ 0) — коэффициенты правильного многочлена 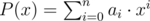 . Гарантируется, что P(2) ≠ 0.
. Гарантируется, что P(2) ≠ 0.
Выведите количество способов изменить ровно один коэффициент многочлена P, так чтобы получить правильный многочлен Q, для которого Q(2) = 0.
3 1000000000
10 -9 -3 5
3
3 12
10 -9 -3 5
2
2 20
14 -7 19
0
В первом примере дан многочлен P(x) = 10 - 9x - 3x2 + 5x3.
Существуют три способа изменить коэффициенты подходящим образом:
- Установить a0 = - 10, так чтобы Q(x) = - 10 - 9x - 3x2 + 5x3. Действительно, Q(2) = - 10 - 18 - 12 + 40 = 0.
- Поменять a2 = - 8. Тогда Q(x) = 10 - 9x - 8x2 + 5x3 и Q(2) = 10 - 18 - 32 + 40 = 0.
- Последний способ — сделать a1 = - 19. Тогда Q(x) = 10 - 19x - 3x2 + 5x3 и Q(2) = 10 - 38 - 12 + 40 = 0.
Во втором примере дан тот же самый многочлен, но значение k равно 12 вместо 109. Первые два способа по прежнему работает, а в третьем получается |a1| > k и соответствующий Q не является правильным. Таким образом, ответ для этого примера равен 2.
| Название |
|---|




