Деревом называется связный неориентированный граф, состоящий из n вершин и n - 1 ребра. Вершины пронумерованы целыми числами от 1 до n.
У полярного медвежонка Лимака было дерево, но он его потерял. Однако он всё ещё помнит о нём некоторые факты.
Вам даны m пар вершин (a1, b1), (a2, b2), ..., (am, bm). Лимак точно помнит, что между вершинами ai и bi не было ребра. Помимо этого, он помнит, что в дереве было ровно k рёбер инцидентных вершин 1 (степень вершины 1 равнялась k).
Проверьте, существует ли хотя бы одно дерево, подходящее под описание Лимака.
В первой строке входных данных записаны три числа n, m и k (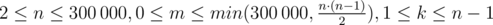 ) — количество вершин в дереве Лимака, количество запрещённых пар вершин и степень вершины 1 соответственно.
) — количество вершин в дереве Лимака, количество запрещённых пар вершин и степень вершины 1 соответственно.
В i-й из следующих m строк записаны два различных числа ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi) — i-я запрещённая пара. Гарантируется, что каждая пара вершин встречается во входных данных не более одного раза.
Если существует хотя бы одно дерево, подходящее под описание Лимака, то выведите «possible» (без кавычек). В противном случае выведите «impossible» (без кавычек).
5 4 2
1 2
2 3
4 2
4 1
possible
6 5 3
1 2
1 3
1 4
1 5
1 6
impossible
В первом примере дерево состоит из 5 вершин. Степень вершины 1 должна быть равна 2. Все условия будут выполнены для дерева, состоящего из рёбер 1 - 5, 5 - 2, 1 - 3 и 3 - 4.
Во втором примере Лимак помнит, что не существовало рёбер 1 - 2, 1 - 3, 1 - 4, 1 - 5 и 1 - 6. Таким образом, вершина 1 не могла быть соединена ни с одной другой вершиной, и подходящего дерева не существует.
| Название |
|---|




