Дан неориентированный граф из n вершин и m рёбер. Каждое из рёбер графа изначально покрашено либо в красный, либо в синий цвет. За один ход разрешается выбрать произвольную вершину, и изменить цвета всех инцидентных ей рёбер, то есть все красные рёбра, заканчивающиеся в этой вершине, становятся синими, и наоборот, все синие становятся красными.
Найдите кратчайшую последовательность ходов, после выполнения которой все рёбра графа будут покрашены в один цвет.
В первой строке входных данных записаны два числа n и m (1 ≤ n, m ≤ 100 000) — количество вершин и количество рёбер в графе соответственно.
Следующие m строк задают ребра графа, i-я из них содержит два числа ui и vi ci (1 ≤ ui, vi ≤ n, ui ≠ vi) — номера вершин, соединённых i-м ребром, и символ ci (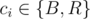 ), определяющий цвет данного ребра. Если ci равняется 'R', то данное ребро изначально красное, а если 'B', то синее. Гарантируется, что граф не содержит петель и кратных рёбер.
), определяющий цвет данного ребра. Если ci равняется 'R', то данное ребро изначально красное, а если 'B', то синее. Гарантируется, что граф не содержит петель и кратных рёбер.
Если не существует способа сделать цвета всех рёбер одинаковыми, то выведите - 1 в единственной строке выходных данных. В противном случае сначала выведите k — минимальное необходимое число ходов, а затем выведите k чисел a1, a2, ..., ak, где ai равняется номеру вершины, выбираемой на i-м ходу.
Если подходящих оптимальных последовательностей несколько, то разрешается вывести любую из них.
3 3
1 2 B
3 1 R
3 2 B
1
2
6 5
1 3 R
2 3 R
3 4 B
4 5 R
4 6 R
2
3 4
4 5
1 2 R
1 3 R
2 3 B
3 4 B
1 4 B
-1
| Название |
|---|




