| Codeforces Round 363 (Div. 1) |
|---|
| Закончено |
Два положительных целых числа взаимно просты, если их наибольший общий делитель равен 1.
Один медвежонок не хочет говорить Радевушу, как решается одна алгоритмическая задача, поэтому Радевуш решил взломать сейф медвежонка с решениями. Чтобы открыть дверь, требуется ввести в качестве кода перестановку целых чисел от 1 до n. Дверь откроется, только если для перестановки выполнится следующее условие:
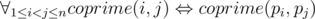
Другими словами, два элемента взаимно просты, если и только если их индексы взаимно просты.
Некоторые элементы перестановки уже выбраны. Сколько существует способов заполнить оставшиеся позиции так, чтобы сейф открылся? Найдите остаток от деления этого числа на 109 + 7.
В первой строке входных данных записано число n (2 ≤ n ≤ 1 000 000) — количество элементов в перестановке.
Во второй строке записаны n целых чисел p1, p2, ..., pn (0 ≤ pi ≤ n), причём pi = 0 означает, что это место ещё свободно, а pi ≥ 1 означает определённое число.
Гарантируется, что если i ≠ j и pi, pj ≥ 1, то pi ≠ pj.
Выведите остаток от деления количества способов заполнить оставшиеся позиции на 109 + 7 (то есть ответ по модулю 1 000 000 007).
4
0 0 0 0
4
5
0 0 1 2 0
2
6
0 0 1 2 0 0
0
5
5 3 4 2 1
0
В первом примере все четыре элемента перестановки ещё не определены. Поставленным условиям удовлетворяют четыре перестановки: (1, 2, 3, 4), (1, 4, 3, 2), (3, 2, 1, 4) и (3, 4, 1, 2).
Во втором примере уже определены p3 = 1 и p4 = 2. Условие выполнится для двух перестановок (3, 4, 1, 2, 5) и (5, 4, 1, 2, 3).
| Название |
|---|




