| Codeforces Round 372 (Div. 1) |
|---|
| Закончено |
Кодеру ZS'у даны две перестановки p и q множества {1, 2, ..., n}, но некоторые из их элементов заменены 0. Расстояние между двумя перестановками p и q определяется как минимальное количество обменов двух элементов, необходимое, чтобы превратить p в q. ZS может менять местами только любые два элемента перестановки p.
Кодер ZS хочет найти количество способов заменить нули положительными целыми числами из множества {1, 2, ..., n} так, что p и q будут являться перестановками {1, 2, ..., n}, а расстояние между p и q в точности равно k.
Кодер ZS хочет найти ответ для всех 0 ≤ k ≤ n - 1. Поможете ему?
Первая строка входных данных содержит целое число n (1 ≤ n ≤ 250) — количество элементов в перестановках.
Вторая строка содержит n целых чисел, p1, p2, ..., pn (0 ≤ pi ≤ n) — перестановка p. Гарантируется, что существует хотя бы один способ заменить нули так, что p станет перестановкой {1, 2, ..., n}.
Вторая строка содержит n целых чисел, q1, q2, ..., qn (0 ≤ qi ≤ n) — перестановка q. Гарантируется, что существует хотя бы один способ заменить нули так, что q станет перестановкой {1, 2, ..., n}.
Выведите n целых чисел, i-е из них должно соответствовать ответу для k = i - 1. Так как ответ может быть довольно большим, а Кодер ZS любит странные простые числа, выведите ответы по модулю 998244353 = 223·7·17 + 1, который является простым.
3
1 0 0
0 2 0
1 2 1
4
1 0 0 3
0 0 0 4
0 2 6 4
6
1 3 2 5 4 6
6 4 5 1 0 0
0 0 0 0 1 1
4
1 2 3 4
2 3 4 1
0 0 0 1
В первом примере из условия существует всего один способ заменить нули так, что потребуется 0 обменов для превращения p в q — это p = (1, 2, 3), q = (1, 2, 3).
Существует два способа заменить нули так, что требуется 1 обмен для превращения p в q. Один из них — p = (1, 2, 3), q = (3, 2, 1), тогда обмен 1 и 3 в p превращает ее в q. Другой способ — p = (1, 3, 2), q = (1, 2, 3). В этом случае работает обмен 2 и 3.
Наконец, существует всего один способ заменить нули так, что потребуется 2 обмена для превращения p в q — p = (1, 3, 2), q = (3, 2, 1). Тогда мы можем превратить p в q вот так: 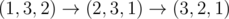 .
.
| Название |
|---|




