| Bubble Cup 9 - Finals [Online Mirror] |
|---|
| Закончено |
Герои Могущие Магию идут по прямой дороге и сражаются с бесами. Бесы слабые и уязвимые существа, и не являются интересными соперниками, но нашим героям нравится с ними сражаться. Потому что это весело.
Герой Игнатиус просто обожает бесов. Перед ним находится прямая с бесами, которая может быть представлена как массив целых чисел a длины n (в индексации с 0), где ai означает количество бесов в позиции i. Иногда из ниоткуда появляются новые бесы. Когда герой собирается сражаться с бесами, он выбирает некоторый отрезок данной прямой, начинает в одном конце отрезка и заканчивает в другом, ни в какой момент не покидая отрезок. Герой может перемещаться на одну позицию влево или на одну позицию вправо. Каждый раз, когда герой выполняет перемещение, он убивает одного беса в клетке, куда он пришёл, то есть количество бесов в этой клетке уменьшается на 1. Также герой убивает одного беса когда только появляется в крайней клетке отрезка в начале маршрута.
Целью героев является победить всех бесов на отрезке и при этом никогда не делать ход в пустую клетку (где нет бесов), потому что это скучно. Игнатиус любит бесов, поэтому он на самом деле их не убивает, так что при подготовке этой задачи ни один бес не пострадал. Однако, он бы хотел, чтобы вы отвечали ему на вопросы, возможно ли зачистить от бесов некоторый отрезок, если действовать согласно правилам выше.
Требуется обработать q различных запросов:
- 1 a b k — k бесов появляются в каждой клетке отрезка [a, b].
- 2 a b — Игнатиус хочет знать, можно ли победить всех бесов на отрезке [a, b], действую согласно описанным выше правилам.
В первой строке записано целое число n (1 ≤ n ≤ 200 000) — длина массива a. Далее следуют n целых чисел a1, a2, ..., an (0 ≤ ai ≤ 5 000), означающих изначальные количества бесов в клетках. В третьей строке записано единственное целое число q (1 ≤ q ≤ 300 000) — количество запросов. Оставшиеся q строк содержат по одному запросу. Каждый запрос определяется целыми числами a, b и, возможно, k (0 ≤ a ≤ b < n, 0 ≤ k ≤ 5 000).
Для каждого запроса второго типа выведите 1, если можно зачистить отрезок по приведённым в условии правилам, и 0 в противном случае.
3
2 2 2
3
2 0 2
1 1 1 1
2 0 2
0
1
В первом запросе невозможно дойти от первой клетки до последней, убив при этом всех бесов и не заскучав. Когда к значению второй клетки добавляется 1, это становится возможным, например, если двигаться следующим маршрутом: 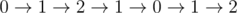 .
.
| Название |
|---|




