| Codeforces Round 385 (Div. 1) |
|---|
| Закончено |
Наконец-то Коровоконг стал правителем мира и теперь может навести в нём порядок. Для начала он хочет, чтобы людям было как можно более удобно путешествовать внутри своих стран.
Представим мир как неориентированный граф из n вершин (городов) и m рёбер (дорог). k из этих вершин являются столицами государств (по одной столице для каждой из k стран).
Любая пара вершин соединена не более чем одним ребром, и никакое ребро не соединяет вершину саму с собой. Более того, для любых двух вершин, являющихся столицами, не существует пути между этими двумя вершинами. Любой граф, удовлетворяющий всем этим условиям, называется стабильным.
Коровоконг хочет добавить в граф как можно больше рёбер, так чтобы он всё ещё оставался стабильным. Выясните, сколько рёбер он может добавить.
В первой строке входных данных записаны три числа n, m и k (1 ≤ n ≤ 1 000, 0 ≤ m ≤ 100 000, 1 ≤ k ≤ n) – количество вершин и рёбер в графе, а также количество вершин, являющихся столицами.
Во второй строке записаны k различных целых чисел c1, c2, ..., ck (1 ≤ ci ≤ n), означающих номера вершин, являющихся столицами.
В каждой из последующих m строк записаны два целых числа ui и vi (1 ≤ ui, vi ≤ n), означающих рёбра неориентированного графа.
Гарантируется, что описанный во входных данных граф является стабильным.
Выведите одно целое число — максимальное количество рёбер, которое Коровоконг может добавить в имеющийся граф, чтобы он остался стабильным.
4 1 2
1 3
1 2
2
3 3 1
2
1 2
1 3
2 3
0
В первом примере граф выглядит следующим образом:
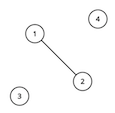
Во втором примере граф выглядит следующим образом:
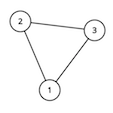
| Название |
|---|




