| Codeforces Round 388 (Div. 2) |
|---|
| Закончено |
Дана перестановка целых чисел от 1 до n. Ровно один раз с перестановкой проделывается следующее преобразование: выбирается некоторый случайный отрезок и все его элементы перемешиваются. Формально:
- Выбирается случайный подотрезок (непрерывная подпоследовательность) от l до r включительно. При этом все
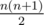 отрезков равновероятны.
отрезков равновероятны. - Пусть k = r - l + 1, то есть длине выбранного отрезка. Выбирается случайная перестановка чисел от 1 до k, p1, p2, ..., pk. При этом все k! перестановок равновероятны.
- К элементам отрезка применяется данная перестановка, то есть перестановка a1, a2, ..., al - 1, al, al + 1, ..., ar - 1, ar, ar + 1, ..., an переходит в перестановку a1, a2, ..., al - 1, al - 1 + p1, al - 1 + p2, ..., al - 1 + pk - 1, al - 1 + pk, ar + 1, ..., an.
Инверсией в перестановке называется пара элементов (не обязательно соседних), нарушающих порядок сортировки по возрастанию, то есть количество инверсий равно количеству пар (i, j), таких что i < j и ai > aj. Найдите математическое ожидание количества инверсий после выполнения данной операции.
В первой строке записано целое число n (1 ≤ n ≤ 100 000) — длина перестановки.
Во второй строке записано n различных целых чисел от 1 до n — элементы перестановки.
Выведите единственное вещественное число — математическое ожидание количества инверсий. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 9.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 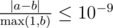 .
.
3
2 3 1
1.916666666666666666666666666667
| Название |
|---|




