| 8VC Venture Cup 2017 - Elimination Round |
|---|
| Закончено |
У Польшара есть выпуклый многоугольник с n вершинами, причем никакие три его диагонали не пересекаются в одной точке. Польшар захотел улучшить его, нарисовав несколько красных отрезков.
Он выбрал число k такое, что gcd(n, k) = 1 и пронумеровал вершины многоугольника от 1 до n в порядке обхода по часовой стрелке. Польшар затем повторил следующее действие n раз, стартуя с вершины номер 1:
Пусть вы закончили предыдущее действие в вершине x (положим x = 1, если текущее действие первое). Нарисуйте отрезок, соединяющий вершину x с k-й следующей вершиной в порядке обхода по часовой стрелке. Это будет либо вершина x + k, либо вершина x + k - n в зависимости от того, какое из этих чисел является корректным номером вершины.
Ваша задача состоит в том, чтобы посчитать число секций многоугольника после каждого действия. Секцией называется чистая площадь внутри многоугольника, ограниченная нарисованными диагоналями или сторонами многоугольника.
Единственная строка содержит два числа n и k (5 ≤ n ≤ 106, 2 ≤ k ≤ n - 2, gcd(n, k) = 1).
Выведите n чисел. i-е из них должно быть равно числу секций после того, как будут нарисованы первые i отрезков.
5 2
2 3 5 8 11
10 3
2 3 4 6 9 12 16 21 26 31
Наибольший общий делитель (gcd) двух чисел a и b равен наибольшему натуральному числу, делящему и a, и b без остатка.
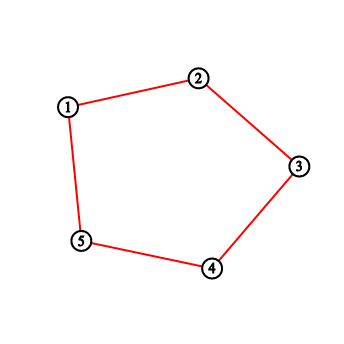
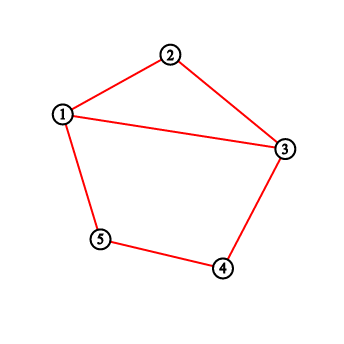
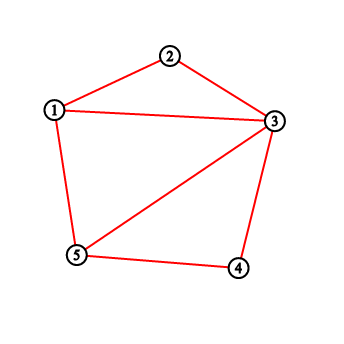
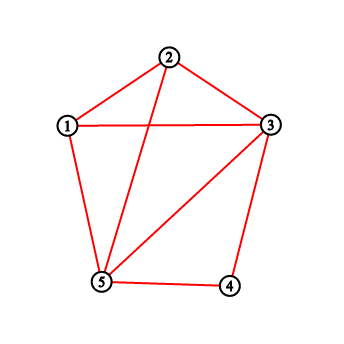
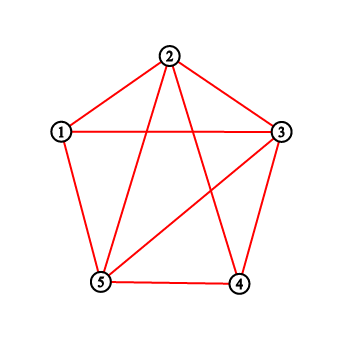
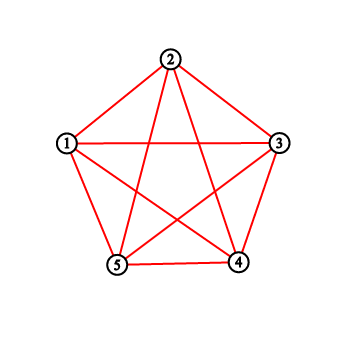
В первом примере вы должны вывести «2 3 5 8 11». Рисунки соответствуют ситуации до и после каждой нарисованной линии.
| Название |
|---|




