| VK Cup 2017 - Раунд 2 |
|---|
| Закончено |
Вам дано n целых чисел a1, a2, ..., an. Обозначим этот список как T.
Пусть f(L) — функция, аргументом которой является непустой список чисел L.
Результатом функции является целое число, вычисленное по следующим правилам:
- Сначала все числа из L дополняются ведущими нулями, чтобы они имели одинаковую длину, равную максимальной длине среди чисел в L.
- Затем строится строка, где символ номер i является минимальным из i-х символов в дополненных нулями исходных числах.
- Полученная строка понимается как число, записанное в десятичной системе счисления, которое и является результатом функции.
Например, f(10, 9) = 0, f(123, 321) = 121, f(530, 932, 81) = 30.
Определим функцию
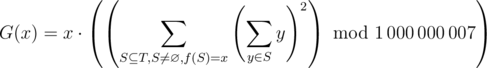
означает подпоследовательность.Другими словами, G(x) — сумма квадратов сумм элементов непустых подпоследовательностей T, для которых функция f возвращает x, по модулю 1 000 000 007, в конце умноженная на x. Результат последнего умножения не берется по модулю.
Вы хотите вычислить G(0), G(1), ..., G(999 999). Для уменьшения размера вывода вычислите одно число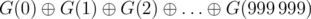 
, где 
означает побитовое исключающее ИЛИ.
Первая строка содержит одно целое число n (1 ≤ n ≤ 1 000 000) — число элементов в списке T.
Вторая строка содержит n целых чисел a1, a2, ..., an (0 ≤ ai ≤ 999 999) — элементы списка.
Выведите единственное число — ответ на задачу.
3
123 321 555
292711924
1
999999
997992010006992
10
1 1 1 1 1 1 1 1 1 1
28160
В первом примере ненулевые значения G равны: G(121) = 144 611 577, G(123) = 58 401 999, G(321) = 279 403 857, G(555) = 170 953 875. Побитовое исключающее ИЛИ этих чисел равно 292 711 924.
Например,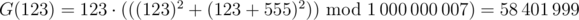 
, потому что функция f над последовательностями [123] и [123, 555] производит результат 123.
Во втором примере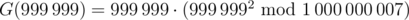 
В последнем пример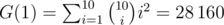е 
, где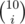 
— биномиальный коэффициент.
