| Tinkoff Challenge - Elimination Round |
|---|
| Закончено |
Раньше, когда не было интернета, у каждого банка было множество отделений по всему городу Банкополису, что вызывало множество проблем. А именно, в каждом отделении нужно было каждый день проводить инкассацию.
Однажды Олег услышал разговор двух инкассаторов одного банка. Они каждый день объезжали все отделения и офисы этого банка, причем двигались они по строго определенной схеме. Инкассаторы выезжали из центрального офиса, и каждый раз перемещались по специальной дороге либо между двумя офисами, либо между каким-то офисом и каким-то отделением, в итоге возвращаясь обратно в центральный офис. Известно, что всего отделений и офисов было было n, а специальных дорог — на одну меньше, то есть n - 1. Иными словами, система специальных дорог образовывала корневое дерево, корнем которого являлся центральный офис, все листья дерева были отделениями, а все внутренние вершины — офисами. Инкассаторы всегда объезжали офисы и отделения по одному и тому же маршруту, число дорог в котором было минимально возможным, то есть 2n - 2.
Один из инкассаторов утверждал, что между посещениями отделения a и отделения b (в таком порядке) они посещают столько же отделений, что и между посещениями отделений b и затем a. Другой инкассатор утверждал, что между посещениями отделения c и отделения d они посещают столько же отделений, что и между посещениями отделений d и затем c. Интересной особенностью разговора было то, что кратчайший путь по специальным дорогам между любой парой отделений из a, b, c и d проходил через центральный офис.
Зная схему дорог и номера отделений a, b, c и d, определите, могла ли происходить ситуация, описанная инкассаторами, или нет.
В первой строке находится одно целое число n (5 ≤ n ≤ 5000) — общее число отделений и офисов. Отделения и офисы пронумерованы от 1 до n, центральный офис имеет номер 1.
На следующей строке находятся четыре различных целых числа a, b, c или d (2 ≤ a, b, c, d ≤ n) — номера отделений, упомянутые в разговоре инкассаторов. Гарантируется, что все эти номера являются отделениями (то есть листьями дерева), а не офисами. Гарантируется, что кратчайший путь между любой парой из этих отделений проходит через центральный офис.
Далее следуют n - 1 чисел p2, p3, ..., pn (1 ≤ pi < i), где pi обозначает, что существует специальная дорога между i-м офисом и pi-м офисом или отделением.
Заметьте, что у отделений и офисов общая нумерация.
Гарантируется, что заданный граф является деревом. Отделениями являются листья этого дерева, а офисами — внутренние вершины.
Если ситуация, описанная инкассаторами, возможна, выведите «YES». Иначе выведите «NO».
5
2 3 4 5
1 1 1 1
YES
10
3 8 9 10
1 2 2 2 2 2 1 1 1
NO
13
13 12 9 7
1 1 1 1 5 5 2 2 2 3 3 4
YES
В первом примере возможен следующий маршрут инкассаторов 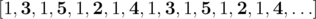 . Можно заметить, что между посещениями отделений a и b инкассаторы посещают столько же отделений, сколько между посещениями отделениями b и a; аналогичная ситуация с отделениями c и d (маршрут инкассаторов является бесконечным и периодичным, но порядок посещения офисов и отделений не меняется изо дня в день и всегда строго фиксирован).
. Можно заметить, что между посещениями отделений a и b инкассаторы посещают столько же отделений, сколько между посещениями отделениями b и a; аналогичная ситуация с отделениями c и d (маршрут инкассаторов является бесконечным и периодичным, но порядок посещения офисов и отделений не меняется изо дня в день и всегда строго фиксирован).
Во втором примере не существует такого порядка посещения офисов и отделений, что между посещениями c и d инкассаторы заедут в столько же отделений, что между посещениями d и c, а значит, ответа не существует.
В третьем примере маршрут, удовлетворяющий условию задачи, такой: 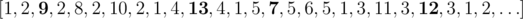 .
.
| Название |
|---|