| Codeforces Round 411 (Div. 1) |
|---|
| Закончено |
Паша — прилежный студент, один из лучших друзей Моджака. Он всегда размышляет над какой-то задачей. Сегодня они разговаривали о следующей задаче.
Дан лес (ациклический неориентированный граф) из n вершин и m ребер. Также есть q запросов, на которые необходимо ответить. В каждом запросе даны две вершины v и u. Пусть V — множество вершин в компоненте связности, к которой принадлежит v, а U — множество вершин в компоненте связности, к которой принадлежит u. Добавим ребро между некоторой вершиной 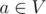 и некоторой вершиной
и некоторой вершиной 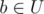 и вычислим величину d получившейся компоненты. Если получившаяся компонента — дерево, то величина d равна диаметру компоненты, иначе она равна -1. Найдите математическое ожидание величины d, если вершины a и b выбираются из множеств равновероятно случайным образом.
и вычислим величину d получившейся компоненты. Если получившаяся компонента — дерево, то величина d равна диаметру компоненты, иначе она равна -1. Найдите математическое ожидание величины d, если вершины a и b выбираются из множеств равновероятно случайным образом.
Можете помочь Паше решить эту задачу?
Диаметром компоненты называется максимальное расстояние между парой вершин в компоненте. Расстоянием между двумя вершинами называется минимальное число ребер на пути между ними.
Заметьте, что запросы не добавляют ребер в изначальный лес.
Первая строка содержит три целых числа n, m и q (1 ≤ n, m, q ≤ 105) — количество вершин и ребер в графе и количество запросов.
Каждая из следующих m строк содержит два целых числа ui и vi (1 ≤ ui, vi ≤ n), что значит, что есть ребро между вершинами ui и vi.
Гарантируется, что заданный граф — лес.
Каждая из следующих q строк содержит два целых числа ui и vi (1 ≤ ui, vi ≤ n) — вершины, участвующие в i-м запросе.
Для каждого запроса выведите математическое ожидание величины d в соответствии с условием задачи.
Ваш ответ будет засчитан, если его абсолютная или относительная ошибка не превосходит10 - 6. Формально, пусть ваш ответ равен a, а ответ жюри равен b. Ваш ответ будет засчитан, если 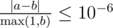 .
.
3 1 2
1 3
3 1
2 3
-1
2.0000000000
5 2 3
2 4
4 3
4 2
4 1
2 5
-1
2.6666666667
2.6666666667
В первом примере вершины 1 и 3 лежат в одной компоненте, поэтому ответ на первый запрос равен -1. Во втором запросе есть два исхода: добавить ребро 1 - 2, или добавить ребро 2 - 3. В обоих случаях диаметр равен 2, поэтому ответ равен 2.
Во втором примере ответ на первый запрос равен -1. Ответ на второй запрос — среднее по трем случаям: Если добавлены ребра 1 - 2 или 1 - 3, то диаметр будет равен 3, а если добавлено ребро 1 - 4, то диаметр равен 2. Поэтому ответ равен 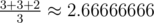 .
.
| Название |
|---|




