| Codeforces Round 415 (Div. 1) |
|---|
| Закончено |
Устав от скучных свиданий, Леха и Нура решили сыграть в игру.
Леха раздобыл дерево из n вершин, пронумерованных от 1 до n. Напомним, что дерево — это связный неориентированный граф без циклов. На каждой вершине v дерева записано некоторое число av. Совершенно случайно оказалось, что все значения, записанные на вершинах, различны и являются натуральными числами от 1 до n.
Игра происходит следующим образом. Нура случайно и равновероятно выбирает некоторую вершину u дерева и передает ход Лехе. Леха, в свою очередь, случайно и равновероятно выбирает некоторую вершину v из оставшихся вершин дерева (v ≠ u). Как несложно догадаться, существует n(n - 1) вариантов выбора вершин игроками. Затем игроки вычисляют значение функции f(u, v) = φ(au·av) · d(u, v) от выбранных вершин, где φ(x) — функция Эйлера, а d(x, y) — кратчайшее расстояние между вершинами x и y в дереве.
Совсем скоро игра наскучила Нуре, поэтому Леха, чтобы разрядить обстановку, решил посчитать математическое ожидание значения функции f по всем вариантам выбора вершин u и v в надежде хоть как-то удивить девушку.
Леха просит вас помочь ему посчитать искомое математическое ожидание. Пусть данное значение представимо в виде несократимой дроби 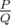 . Чтобы еще больше удивить Нуру, он хочет назвать ей значение
. Чтобы еще больше удивить Нуру, он хочет назвать ей значение 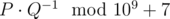 .
.
Помогите Лехе!
Первая строка содержит одно целое число n (2 ≤ n ≤ 2·105) — количество вершин в дереве, раздобытом Лехой.
Вторая строка содержит n разделенных пробелами целых различных чисел a1, a2, ..., an (1 ≤ ai ≤ n) — значения, записанные на вершинах дерева.
Каждая из следующих n - 1 строк содержит по два целых числа x и y (1 ≤ x, y ≤ n), описывающих очередное ребро дерева. Гарантируется, что данный набор ребер описывает дерево.
В единственной строке выведите число, равное P·Q - 1 по модулю 109 + 7.
3
1 2 3
1 2
2 3
333333338
5
5 4 3 1 2
3 5
1 2
4 3
2 5
8
Функция Эйлера φ(n) — это количество таких i, что 1 ≤ i ≤ n, что gcd(i, n) = 1, где gcd(x, y) — наибольший общий делитель чисел x и y.
В первом примере существует 6 вариантов выбора вершин Лехой и Нурой:
- u = 1, v = 2, f(1, 2) = φ(a1·a2)·d(1, 2) = φ(1·2)·1 = φ(2) = 1
- u = 2, v = 1, f(2, 1) = f(1, 2) = 1
- u = 1, v = 3, f(1, 3) = φ(a1·a3)·d(1, 3) = φ(1·3)·2 = 2φ(3) = 4
- u = 3, v = 1, f(3, 1) = f(1, 3) = 4
- u = 2, v = 3, f(2, 3) = φ(a2·a3)·d(2, 3) = φ(2·3)·1 = φ(6) = 2
- u = 3, v = 2, f(3, 2) = f(2, 3) = 2
Искомое математическое ожидание равно 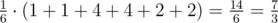 . Значение, которым Леха хочет удивить Нуру, равно 7·3 - 1 = 7·333333336 = 333333338
. Значение, которым Леха хочет удивить Нуру, равно 7·3 - 1 = 7·333333336 = 333333338 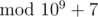 .
.
Во втором примере математическое ожидание равно 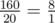 , следовательно, Лехе придется удивлять Нуру числом 8·1 - 1 = 8
, следовательно, Лехе придется удивлять Нуру числом 8·1 - 1 = 8 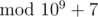 .
.
| Название |
|---|




