Вам дан строго выпуклый многоугольник из n вершин. Гарантируется, что никакие три точки не лежат на одной прямой. Вы хотите пройти максимальный путь по многоугольнику без самопересечений, который посещает каждую из вершин не более одного раза.
Конкретнее, ваш путь должен представлять из себя последовательность различных точек, вы пройдете по отрезкам прямых, соединяющих соседние по порядку точки. Эти отрезки не могут касаться или пересекаться, кроме как в точках вашей последовательности.
По данному многоугольнику найдите максимальный по длине путь такой, который посещает каждую из вершин не более одного раза.
Первая строка содержит целое число n (2 ≤ n ≤ 2 500) — количество точек.
Следующие n строк содержат по два целых числа xi, yi (|xi|, |yi| ≤ 109), обозначающих координаты i-й вешины многоугольника.
Гарантируется, что задан строго выпуклый многоугольник в порядке обхода по часовой стрелке.
Выведите одно вещественное число, обозначающее длину максимального по длине пути, посещающего каждую из вершин не более одного раза.
Ваш ответ будет считаться корректным, если его абсолютная или относительная ошибка составляет не более 10 - 9. А именно, если ваш ответ равен a, а ответ жюри равен b, ваш ответ будет зачтен, если 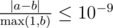 .
.
4
0 0
0 1
1 1
1 0
3.4142135624
Один из оптимальных путей — пройти по вершинам 0,1,3,2 в таком порядке.
| Название |
|---|




