В компьютерной сети Берляндского государственного университета имеется n маршрутизаторов, пронумерованных от 1 до n. Некоторые пары маршрутизаторов соединены коммутационными шнурами (патч-кордами). Информация по патч-корду может передаваться в любом из двух направлений. Сеть устроена таким образом, что между любыми двумя маршрутизаторами возможна передача информации (непосредственно или через другие маршрутизаторы). В сети отсутствуют циклы, поэтому между каждой парой маршрутизаторов существует единственный путь по патч-кордам.
К сожалению, точная топология сети была утеряна администраторами. С целью её восстановления была собрана следующая вспомогательная информация.
Для каждого патч-корда p, непосредственно присоединённого к маршрутизатору i, известны все маршрутизаторы, находящиеся за патч-кордом p относительно i. Иными словами, известны все маршрутизаторы, путь от которых до маршрутизатора i включает в себя патч-корд p. Таким образом, для каждого маршрутизатора i составлены ki списков, где ki — количество патч-кордов, подключенных к i.
Например, пусть сеть состоит из трех маршрутизаторов, соединённых в цепочку 1 - 2 - 3. Тогда:
- маршрутизатор 1: для единственного патч-корда, присоединённого к первому маршрутизатору, составлен единственный список, который содержит два маршрутизатора: 2 и 3;
- маршрутизатор 2: для каждого из патч-кордов, присоединённых ко второму маршрутизатору, составлено по списку: один из них содержит маршрутизатор 1, а другой — маршрутизатор 3;
- маршрутизатор 3: для единственного патч-корда, присоединённого к третьему маршрутизатору, составлен один список, который содержит два маршрутизатора: 1 и 2.
Помогите администраторам компьютерной сети БГУ восстановить топологию сети, то есть определить все пары маршрутизаторов, непосредственно соединенные патч-кордами.
В первой строке содержится целое число n (2 ≤ n ≤ 1000) — количество маршрутизаторов в сети БГУ.
В каждой из следующих n строк содержатся описания списков для очередного маршрутизатора. Так, i-я строка содержит списки для i-го маршрутизатора.
Описание каждого списка начинается с количества маршрутизаторов в нём. Затем следует символ ':', а после него через запятую перечисляются номера всех маршрутизаторов из списка. Описания списков для каждого патч-корда разделяются символом '-'.
Гарантируется, что для каждого маршрутизатора суммарное количество маршрутизаторов во всех списках равно n - 1, причём все числа в списках каждого маршрутизатора различны. Списки каждого маршрутизатора не содержат номер этого маршрутизатора.
Если решения не существует, выведите -1.
В противном случае в первую строку выведите число n - 1 — количество патч-кордов в сети. В каждой из следующих n - 1 строк выведите по два целых числа — описания патч-кордов в виде номеров соединяемых ими маршрутизаторов. Информация о каждом патч-корде должна быть выведена ровно один раз.
3
2:3,2
1:1-1:3
2:1,2
2
2 1
2 3
5
4:2,5,3,4
1:4-1:1-2:5,3
4:4,5,2,1
4:2,1,3,5
1:3-3:4,2,1
4
2 1
2 4
5 2
3 5
3
1:2-1:3
1:1-1:3
1:1-1:2
-1
Первый пример разобран в условии.
Ответ для второго примера изображён на рисунке.
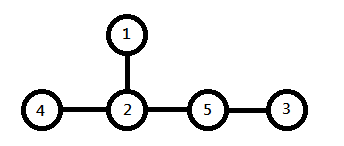
На нём мы можем видеть, что у первого маршрутизатора один список, в котором встречаются все остальные маршрутизаторы. У второго маршрутизатора три списка: в первом — маршрутизатор 4, во втором — маршрутизатор 1, а в третьем — маршрутизаторы 3 и 5. У третьего маршрутизатора один список, в котором встречаются все остальные маршрутизаторы. У четвёртого маршрутизатора тоже один список, в котором встречаются все остальные маршрутизаторы. У пятого маршрутизатора два списка: в первом — маршрутизатор 3, а во втором — маршрутизаторы 1, 2 и 4.
| Название |
|---|




