Иван читает книгу про турниры. Ваня уже знает, что турнир это ориентированный граф с ровно одним ребром между каждой парой вершин. Так же он знает, что очки вершины это число ребер, исходящих из нее.
Кроме определений, Иван узнал про критерий Ландау: существует турнир с последовательностью очков d1 ≤ d2 ≤ ... ≤ dn тогда и только тогда, когда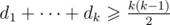 
для всех 1 ≤ k < n и 
.
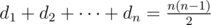Теперь Ваня хочет решить следующую задачу: пусть есть множество чисел S = {a1, a2, ..., am}, существует ли турнир с данным множеством очков? Иными словами, существует ли турнир с последовательностью очков d1, d2, ..., dn, такой, что если убрать повторяющиеся числа, то получим множество {a1, a2, ..., am}?
Если ответ существует, найдите турним с минимальным числом вершин.
Первая строка содержит число m (1 ≤ m ≤ 31).
Следующая строка содержит m различных чисел a1, a2, ..., am (0 ≤ ai ≤ 30) — элементы множества S. Гарантируется, что элементы множества различны.
Если ответа не существует, выведите одну строку «=(» (без кавычек).
Иначе, выведите число n — число вершин в ответе.
После этого выведите n строк из n символов каждая — матрицу смежности турнира. j-й элемент i-й строки должен быть равен 1, если в турнире ребро между вершинами i и j направлено в сторону вершины j, и 0 иначе. Главная диагональ должна содержать только нули.
2
1 2
4
0011
1001
0100
0010
2
0 3
6
000111
100011
110001
011001
001101
000000
