Есть мешок с шарами n различных цветов. В мешке ai шаров цвета i.
Пока в мешке есть хотя бы два шара различных цветов, вы выполняете следующие шаги:
- Возьмите два случайных шара из мешка. Может получиться, что цвета совпали.
- Покрасьте второй шар в цвет первого. Менять порядок шаров не разрешается.
- Положите оба шара обратно в коробку.
- Все эти действия занимают у вас ровно одну секунду.
Пусть M = 109 + 7. Можно доказать, что математическое ожидание времени всего процесса может быть представлено в виде рационального числа 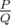 , где P и Q — взаимно простые целые числа, и Q не делится на M. Выведите величину
, где P и Q — взаимно простые целые числа, и Q не делится на M. Выведите величину 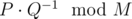 .
.
Первая строка содержит одно целое число n (1 ≤ n ≤ 2 500) — количество цветов.
Вторая строка содержит n целых чисел a1, a2, ..., an (1 ≤ ai ≤ 105) — количество шаров каждого цвета.
Выведите одно число — ответ на задачу.
2
1 1
1
3
1 2 3
750000026
В первом примере независимо от происходящего шары будут одного цвета после одного шага.
Во втором примере есть 6 шаров. Обозначим шары числами от 1 до 6, без ограничения общности, пусть шары 1, 2, 3 изначально имеют цвет 1, шары 4, 5 имеют цвет 2, а шар 6 имеет цвет 3.
Пример того, какой может быть процесс:
- Достали шар 5 и шар 6. Шар 6 становится цвета 2.
- Достали шар 4 и шар 5. Шар 5 остается того же цвета (цвета 2).
- Достали шар 1 и шар 5. Шар 5 становится цвета 1.
- Достали шар 6 и шар 5. Шар 5 становится цвета 2.
- Достали шар 3 и шар 4. Шар 4 становится цвета 1.
- Достали шар 4 и шар 6. Шар 6 становится цвета 1.
- Достали шар 2 и шар 5. Шар 5 становится цвета 1.
Можно показать, что ответ в этом случае равен 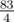 .
.
| Название |
|---|




