| Manthan, Codefest 17 |
|---|
| Закончено |
Нагайна, будучи крестражем Сами-Знаете-Кого, создала армию змей и планирует атаку на Хогвартс.
Вход в школу Хогвартс может быть представлен как прямая линия (ось x) с координатами от 1 до 105. Нагайна запускает змей у входа в Хогвартс. Каждая змея ложится параллельно входу, покрывая некоторый отрезок на расстоянии k от входа от x = l до x = r. Формально, каждая змея может быть представлена как отрезок с концами в точках (l, k) и (r, k). Учтите, что k может быть как положительным, так и отрицательным, но не может быть равно 0.
Пусть для какой-то x-координаты x = i, существую змеи в точке (i, y1) и в точке (i, y2), таких что y1 > 0 и y2 < 0. Тогда если для любой точки (i, y3), содержащей змею и такой, что y3 > 0, выполняется y1 ≤ y3, и для любой точки (i, y4), содержащей змею и такой, что y4 < 0, выполняется |y2| ≤ |y4|, тогда опасность точки x = i равна y1 + |y2|. Если не существует таких y1 или y2 опасность равна 0.
Гарри хочет посчитать опасность некоторых отрезков входа в Хогвартс. Опасность полуинтервала [l, r) может быть вычислена как сумма величин опасностей во всех целых координатах x этого полуинтервала.
Формально, вам необходимо обрабатывать два типа запросов:
- 1 l r k: змея появляется у входа между точками x = l и x = r и координатой y = k (включая l, не включая r).
- 2 l r: вам необходимо узнать опасность полуинтервала с l по r (включая l, не включая r).
В первой строке содержится целое число q (1 ≤ q ≤ 5·104), показывающее число запросов.
Следующие q строк описывают запросы. Описание каждого запроса начинается с типа запроса typei (1 ≤ typei ≤ 2). Затем идёт дальшнейшее описание запросов. Для запросов типа 1 задаются три целых числа li, ri и ki (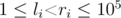 , - 109 ≤ ki ≤ 109, k ≠ 0). Иначе задана пара целых чисел li и ri (1 ≤ li < ri ≤ 105).
, - 109 ≤ ki ≤ 109, k ≠ 0). Иначе задана пара целых чисел li и ri (1 ≤ li < ri ≤ 105).
Для каждого запроса типа 2 выведите ответ.
3
1 1 10 10
1 2 4 -7
2 1 10
34
7
1 2 3 5
1 1 10 10
1 4 5 -5
2 4 8
1 1 10 -10
2 4 8
2 1 10
15
75
170
В первом примере опасность координаты x, равной 1, равна 0, так как не существует y2, удовлетворяющего условию для x = 1.
Опасность x-координат 2 и 3 равна 10 + | - 7| = 17.
Опасность x-координат от 4 до 9 снова 0, так как не существует y2, удовлетворяющего условию.
Таким образом, суммарная опасность равна 17 + 17 = 34.
| Название |
|---|




