| Codeforces Round 435 (Div. 2) |
|---|
| Закончено |
Доктора Зло интересует математика, поэтому он дал Махмуду и Ехабу массив a длины n и массив b длины m. Он рассматривает функцию f(j), которая определена для целых чисел j, удовлетворяющих 0 ≤ j ≤ m - n. Положим ci = ai - bi + j. Тогда f(j) = |c1 - c2 + c3 - c4... cn|. Более формально, 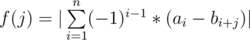 .
.
Доктор Зло хочет, чтобы Махмуд и Ехаб нашли минимальное значение функции для всех допустимых j. Он понимает, что это слишком простая задача, поэтому он решил её усложнить. Он просит их обработать q запросов изменения. Во время каждого запроса Махмуд и Ехаб должны прибавить xi ко всем элементам a в диапозоне [li;ri], то есть прибавить xi к ali, ali + 1, ... , ari. После каждого запроса им требуется посчитать минимальное значение f(j) для всех допустимых j.
Помогите Махмуду и Ехабу.
В первой строке содержатся три целых числа n, m и q (1 ≤ n ≤ m ≤ 105, 1 ≤ q ≤ 105) — количество элементов в a, количество элементов в b и количество запросов, соответственно.
Во второй строке содержатся n целых чисел a1, a2, ..., an. ( - 109 ≤ ai ≤ 109) — элементы a.
В третьей строке содержатся m целых чисел b1, b2, ..., bm. ( - 109 ≤ bi ≤ 109) — элементы b.
В следующих q содержатся описания запросов. Каждая из них содержит три целых числа li ri xi (1 ≤ li ≤ ri ≤ n, - 109 ≤ x ≤ 109) — границы отрезка, на котором происходит обновление и величина, которую необходимо прибавить.
В первой строке выведите минимальное значение функции f до всех запросов.
Затем выведите q строк, в i-й из которых должно содержаться минимальное значение функции f после запроса с номером i.
5 6 3
1 2 3 4 5
1 2 3 4 5 6
1 1 10
1 1 -9
1 5 -1
0
9
0
0
В первом тестовом примере до первого запроса минимум достигается при j = 0 и равен f(0) = |(1 - 1) - (2 - 2) + (3 - 3) - (4 - 4) + (5 - 5)| = |0| = 0.
После первого запроса a становится равным {11, 2, 3, 4, 5}, а минимум достигается при j = 1 и равен f(1) = |(11 - 2) - (2 - 3) + (3 - 4) - (4 - 5) + (5 - 6) = |9| = 9.
После второго запроса a становится равным {2, 2, 3, 4, 5}, минимум достигается при j = 1 и равен f(1) = |(2 - 2) - (2 - 3) + (3 - 4) - (4 - 5) + (5 - 6)| = |0| = 0.
После третьего запроса a становится равным {1, 1, 2, 3, 4}, минимум достигается при j = 0 и равен f(0) = |(1 - 1) - (1 - 2) + (2 - 3) - (3 - 4) + (4 - 5)| = |0| = 0
| Название |
|---|




