| Технокубок 2018 - Отборочный Раунд 2 |
|---|
| Закончено |
На плоскости дано n различных точек с целыми координатами. Для каждой точки можно выполнить одно из трех действий: провести через нее вертикальную прямую, провести через нее горизонтальную прямую или ничего не делать.
Если рассматривать несколько совпадающих прямых как одну, то сколько различных картинок может получиться? Ответ вывести по модулю 109 + 7.
В первой строке дано целое число n (1 ≤ n ≤ 105) — количество точек.
Далее идет n строк. В (i + 1)-й строке даны два целых числа xi, yi ( - 109 ≤ xi, yi ≤ 109) — координаты i-й точки.
Гарантируется, что все точки различны.
Вывести количество различных картинок по модулю 109 + 7.
4
1 1
1 2
2 1
2 2
16
2
-1 -1
0 1
9
В первом примере через точки проходят две вертикальные и две горизонтальные прямые. Существуют способы получить картинку из любого набора этих прямых. В частности, получить картинку на которой нарисованы все четыре прямые можно двумя способами (каждый отрезок обозначает прямую, которой отрезок принадлежит).
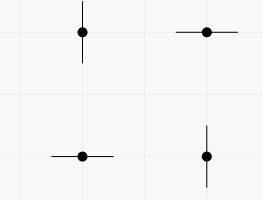 Второй способ:
Второй способ: 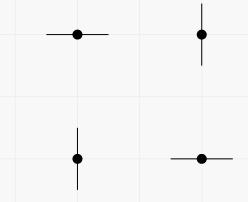
Во втором примере для каждой точки можно независимо выполнить одно из трех действий. Количество картинок равно 32 = 9.
| Название |
|---|




