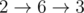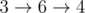| Технокубок 2018 - Отборочный Раунд 2 |
|---|
| Закончено |
→ Виртуальное участие
Виртуальное соревнование – это способ прорешать прошедшее соревнование в режиме, максимально близком к участию во время его проведения. Поддерживается только ICPC режим для виртуальных соревнований.
Если вы раньше видели эти задачи,
виртуальное соревнование не для вас – решайте эти задачи в архиве.
Если вы хотите просто дорешать задачи, виртуальное соревнование не для вас – решайте эти задачи в архиве.
Запрещается использовать чужой код, читать разборы задач и общаться по содержанию соревнования с кем-либо.
→ Теги задачи
структуры данных
теория чисел
*2700
Нет прав на редактирование
→ Материалы соревнования
Условие задачи было недавно изменено. Просмотреть изменения.
×
F. Пути
ограничение по времени на тест
4 секундыограничение по памяти на тест
512 мегабайтввод
стандартный вводвывод
стандартный выводДано положительное целое число n. Построим граф на вершинах 1, 2, ..., n так, чтобы ребро между вершинами u и v существовало тогда и только тогда, когда  . Пусть d(u, v) — кратчайшее расстояние между u и v или 0, если между ними нет пути. Посчитайте сумму d(u, v) для всех 1 ≤ u < v ≤ n.
. Пусть d(u, v) — кратчайшее расстояние между u и v или 0, если между ними нет пути. Посчитайте сумму d(u, v) для всех 1 ≤ u < v ≤ n.
gcd или НОД (наибольший общий делитель) двух натуральных чисел — такое наибольшее натуральное число, которое делит оба этих числа нацело.
Входные данные
Целое число n (1 ≤ n ≤ 107).
Выходные данные
Выведите сумму d(u, v) для всех 1 ≤ u < v ≤ n.
Примеры
Входные данные
6
Выходные данные
8
Входные данные
10
Выходные данные
44
Примечание
Все кратчайшие пути в первом примере:
Между остальными парами вершин путь не существует.
Суммарное расстояние 2 + 1 + 1 + 2 + 1 + 1 = 8.
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 20.11.2024 18:38:09 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|