У Пети было дерево, состоящее из n вершин, пронумерованных целыми числами от 1 до n. Но по стечению обстоятельств он своё дерево потерял.
Петя помнит о k вершинах из своего дерева информацию о расстоянии от каждой из них до всех n вершин дерева.
Перед вами стоит задача восстановить любое дерево, удовлетворяющее информации, которую помнит Петя, либо сообщить, что это невозможно.
В первой строке следуют два целых числа n и k (2 ≤ n ≤ 30 000, 1 ≤ k ≤ min(200, n)) — количество вершин в дереве и количество вершин, о которых помнит Петя.
В следующих k строках содержится информация о вершинах, которую помнит Петя. В i-й строке содержится n целых чисел di, 1, di, 2, ..., di, n (0 ≤ di, j ≤ n - 1), где di, j — расстояние до j-й вершины от i вершины, которую помнит Петя.
Если не существует подходящего дерева, выведите -1.
В противном случае, выведите в n - 1-й строке по два целых числа — концы очередного ребра. Вы можете выводить ребра и концы ребер в любом порядке. Вершины дерева пронумерованы от 1 до n.
Если ответов несколько, разрешается вывести любой из них.
5 2
0 1 2 3 2
2 1 0 1 2
2 1
3 2
4 3
5 2
3 1
1 2 1
-1
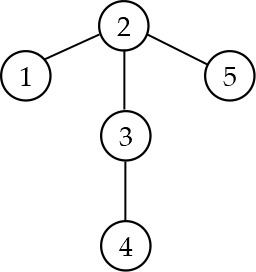
Иллюстрация к первому примеру:
| Название |
|---|




