| Технокубок 2018 - Отборочный Раунд 3 |
|---|
| Закончено |
Дано множество из n точек на плоскости. Назовем прямую, проходящую через начало координат, хорошей, если проекция данного множества точек на эту прямую образует симметричное мультимножество. Найдите количество хороших прямых.
Мультимножество — это множество, в котором разрешается несколько одинаковых элементов.
Мультимножество точек называется симметричным, если существует такая точка P на плоскости, что данное мультимножество обладает центральной симметрией относительно точки P.
В первой строке дано целое число n (1 ≤ n ≤ 2000) — количество точек в данном множестве.
Каждая из следующих n строк содержит два целых числа xi и yi ( - 106 ≤ xi, yi ≤ 106), описывающие координаты точек множества. Гарантируется, что все точки различны.
Если хороших прямых бесконечно много, выведите -1.
Иначе выведите одно целое число — количество хороших прямых.
3
1 2
2 1
3 3
3
2
4 3
1 2
-1
Иллюстрация к первому тесту из условия:
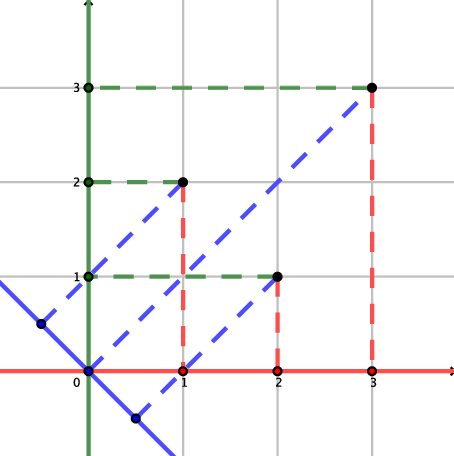
Во втором примере хорошей является любая прямая, проходящая через начало координат.
| Название |
|---|




