| Codeforces Round 446 (Div. 1) |
|---|
| Закончено |
Для заданного связного неориентированного взвешенного графа G минимальным остовным деревом называется подграф G, содержащий все вершины G, являющийся деревом, а также имеющий минимально возможную сумму весов ребер.
Вам дан граф G. Если вы запустите алгоритм по поиску минимального остовного дерева, вы найдете лишь одно минимальное остовное дерево, а другие ребра будут завидовать. Вам дано несколько запросов, каждый запрос содержит подмножество ребер графа G, определите, существует ли минимальное остовное дерево этого графа, содержащее все эти ребра, или нет.
Первая строка содержит два целых числа n, m (2 ≤ n, m ≤ 5·105, n - 1 ≤ m) — количество вершин и ребер в графе, соответственно.
i-я из следующих m строк содержит три целых числа ui, vi, wi (ui ≠ vi, 1 ≤ wi ≤ 5·105) — концы и вес i-го ребра. Возможно, что существует более одного ребра между некоторыми парами вершин. Гарантируется, что данный граф связен.
Следующая строка содержит одно целое число q (1 ≤ q ≤ 5·105) — количество запросов.
Далее следуют q строк, i-я из них содержит описание i-го запроса. Она начинается с целого числа ki (1 ≤ ki ≤ n - 1) — размера подмножества ребер, а затем следуют ki различных целых чисел от 1 до m — индексы ребер в подмножестве. Гарантируется, что сумма значений ki для всех 1 ≤ i ≤ q не превосходит 5·105.
Для каждого запроса выведите «YES» (без кавычек), если существует минимальное остовное дерево со всеми данными ребрами, и «NO» (конечно же, без кавычек) иначе.
5 7
1 2 2
1 3 2
2 3 1
2 4 1
3 4 1
3 5 2
4 5 2
4
2 3 4
3 3 4 5
2 1 7
2 1 2
YES
NO
YES
NO
На рисунке граф из первого примера:
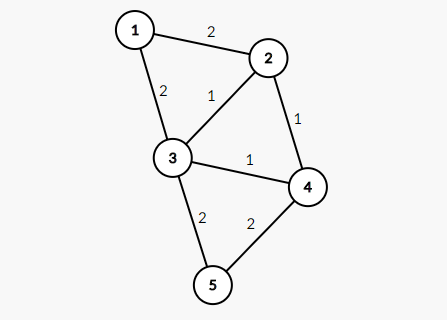
Вес минимального остовного дерева равен 6.
Минимальное остовное дерево из ребер (1, 3, 4, 6) содержит все ребра из первого запроса, поэтому ответ на первый запрос «YES».
Ребра из второго запроса образуют цикл длины 3, поэтому не существует остовного дерева, включающего в себя эти три ребра. Поэтому ответ «NO».
| Название |
|---|




