| Codeforces Round 447 (Div. 2) |
|---|
| Закончено |
Ральф находится в Бинарной стране. Бинарная страна состоит из n городов и (n - 1) двунаправленной дороги, соединяющей города. Дороги пронумерованы от 1 до (n - 1), где i-я дорога соединяет город номер 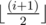 (здесь ⌊ x⌋ обозначает x, округленный вниз к ближайшему целому) и город номер (i + 1), а длина i-й дороги равна Li.
(здесь ⌊ x⌋ обозначает x, округленный вниз к ближайшему целому) и город номер (i + 1), а длина i-й дороги равна Li.
Ральф дал вам m запросов. В каждом запросе он указал некоторый город Ai и целое число Hi. Он хочет сделать несколько поездок, начинающихся в указанном городе. Он может выбрать любой город (включая Ai) в Бинарной стране в качестве конца поездки. От такой поездки он получит (Hi - L) единиц счастья, где L — расстояние между городом Ai и конечным городом маршрута.
Ральфу интересны все поездки из Ai, в которых он может получить положительное количество единиц счастья. Для каждого запроса посчитайте суммарное количество получаемых единиц счастья по всем таким поездкам.
Ральф никогда не проедет по одному и тому же маршруту дважды или больше (в одном запросе), также, он никогда не посетит один город дважды или больше за одну поездку.
Первая строка содержит два целых числа n и m (1 ≤ n ≤ 106, 1 ≤ m ≤ 105).
Далее следуют (n - 1) строк, каждая содержит одно целое число Li (1 ≤ Li ≤ 105) — длину i-й дороги.
Далее следуют m строк, каждая содержит два целых числа Ai и Hi (1 ≤ Ai ≤ n, 0 ≤ Hi ≤ 107).
Выведите m строк, на i-й из них выведите одно целое число — ответ на i-й запрос.
2 2
5
1 8
2 4
11
4
6 4
2
1
1
3
2
2 4
1 3
3 2
1 7
11
6
3
28
Далее следует пояснение ко второму примеру.
Первый запрос Ральфа — начинать поездки в городе 2, а Hi равно 4. Вот варианты поездок, которые у него есть:
- Закончить поездку в городе 5. Так как расстояние между городами 5 и 2 равно 3, он получит 4 - 3 = 1 единицу счастья.
- Закончить поездку в городе 4, тогда он получит 3 единицы счастья.
- Закончить поездку в городе 1, тогда он получит 2 единицы счастья.
- Закончить поездку в городе 3, тогда он получит 1 единицу счастья.
- Обратите внимание, он может закончить поездку в городе 2, тогда он получит 4 единицы счастья.
- Ральф не может закончить поездку в городе 6, так как расстояние между городом 6 и городом 2 равно 5, что приводит к отрицательному количеству единиц счастья.
Поэтому ответ на первый запрос равен 1 + 3 + 2 + 1 + 4 = 11.
| Название |
|---|




