| Codeforces Round 449 (Div. 1) |
|---|
| Закончено |
— Уильям...
— Что случилось?
— Кажется, что-то не так с Сениориусом...
— Я разберусь...

Сениориус изготовлен при помощи соединения специальных талисманов в определённом порядке.
Спустя 500 лет Сениориус находится в плохом состоянии, поэтому Уильям решил полностью его обследовать.
Сениориус сделан из n талисманов, которые Уильям выложил в ряд. На талисмане i написано число ai.
Для того, чтобы починить Сениориус, Уильяму необходимо выполнить m операций, одного из четырёх типов:
- 1 l r x : Для каждого i такого, что l ≤ i ≤ r, ai становится равным ai + x.
- 2 l r x : Для каждого i такого, что l ≤ i ≤ r, ai становится равным x.
- 3 l r x: Вывести x-е по возрастанию число на отрезке [l, r], то есть такое число, которое стояло бы на позиции x в упорядоченном по неубыванию массиве из чисел ai таких, что l ≤ i ≤ r. Гарантируется, что 1 ≤ x ≤ r - l + 1.
- 4 l r x y : Выведите сумму возведённых в степень x чисел ai таких, что l ≤ i ≤ r по модулю y, то есть
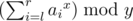 .
.
В первой строке содержатся четыре целых числа n, m, seed, vmax (1 ≤ n, m ≤ 105, 0 ≤ seed < 109 + 7, 1 ≤ vmax ≤ 109).
Тогда тест генерируется следующим псевдокодом:
def rnd():
ret = seed
seed = (seed * 7 + 13) mod 1000000007
return ret
for i = 1 to n:
a[i] = (rnd() mod vmax) + 1
for i = 1 to m:
op = (rnd() mod 4) + 1
l = (rnd() mod n) + 1
r = (rnd() mod n) + 1
if (l > r):
swap(l, r)
if (op == 3):
x = (rnd() mod (r - l + 1)) + 1
else:
x = (rnd() mod vmax) + 1
if (op == 4):
y = (rnd() mod vmax) + 1
Здесь op обозначает тип операции.
Для каждой операции типа 3 или 4 выведите ответ.
10 10 7 9
2
1
0
3
10 10 9 9
1
1
3
3
В первом тестовом примере исходный массив равен {8, 9, 7, 2, 3, 1, 5, 6, 4, 8}.
Дальнейшие операции таковы:
- 2 6 7 9
- 1 3 10 8
- 4 4 6 2 4
- 1 4 5 8
- 2 1 7 1
- 4 7 9 4 4
- 1 2 7 9
- 4 5 8 1 1
- 2 5 7 5
- 4 3 10 8 5
| Название |
|---|




