| Codeforces Beta Round 75 (Div. 1 Only) |
|---|
| Закончено |
В Моржландии собираются построить лыжную базу. Пока проект находится на стадии строительства. Под строительство базы был выбран большой участок земли, на котором находится n лыжных перекрестков. Изначально эти перекрестки никак не соединены.
В процессе строительства будет проложено m двусторонних лыжных дорог. Дороги строятся по очереди: вначале будет построена дорога с номером 1, потом дорога с номером 2, и так далее. Дорога с номером i соединяет перекрестки с номерами ai и bi.
Трасса — это маршрут, обладающий следующими свойствами:
- Маршрут замкнут, то есть он начинается и заканчивается в одном и том же перекрестке.
- Маршрут содержит хотя бы одну дорогу.
- Маршрут не проходит по одной дороге более одного раза, но при этом может проходить через любой перекресток сколько угодно раз.
Будем называть лыжной базой непустое множество дорог, которое можно разбить на одну или более трасс так, чтобы по каждой дороге этого множества проходила ровно одна трасса, при этом каждая трасса может состоять только из дорог выбранного множества. Лыжная база может быть несвязной.
Две лыжные базы считаются различными, если они состоят из разных множеств дорог.
После постройки каждой новой дороги правительство Моржландии хочет знать количество вариантов выбрать лыжную базу на основе некоторого подмножества из уже построенных дорог. Правительство просит вашей помощи в решении данной задачи.
В первой строке находятся два целых числа n и m (2 ≤ n ≤ 105, 1 ≤ m ≤ 105) — количество перекрестков и количество дорог соответственно. Далее в m строках следует описание дорог в порядке их постройки. Каждая дорога описывается парой целых чисел ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi) — номерами соединяемых перекрестков. Между парой перекрестков может быть более одной дороги.
Выведите m строк: i-ая строка должна обозначать количество способов построить лыжную базу после окончания строительства дороги с номером i. Числа следует выводить по модулю 1000000009 (109 + 9).
3 4
1 3
2 3
1 2
1 2
0
0
1
3
Пусть у нас 3 перекрестка и уже построены 4 дороги между перекрестками (как после построки всех дорог в примере): 1 и 3, 2 и 3, 2 дороги между перекрестками 1 и 2. Участок под постройку будет выглядеть следующим образом:
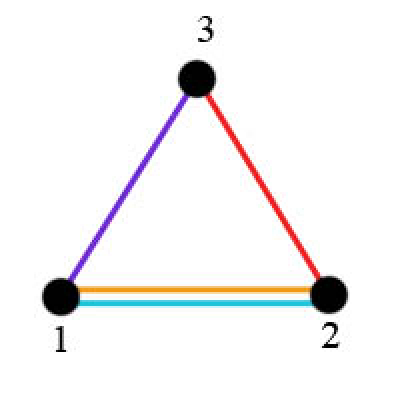
Можно выбрать подмножество дорог 3мя способами:
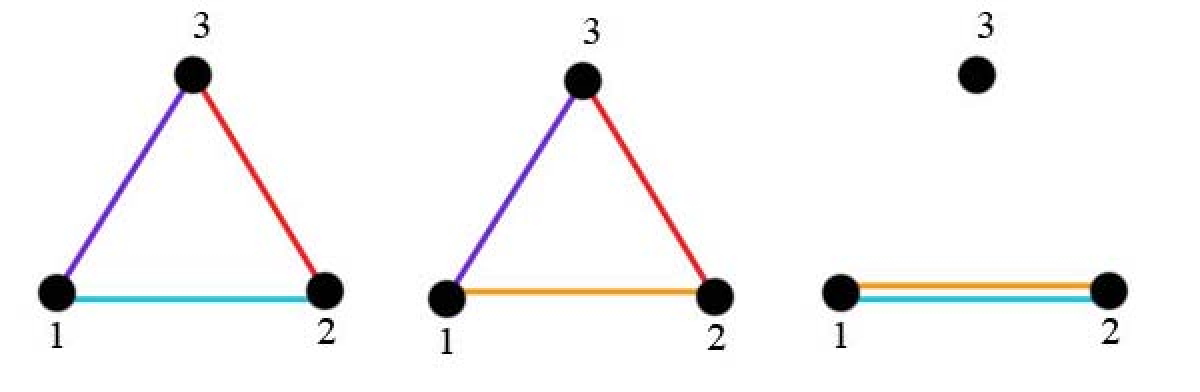
В первом и втором способах можно выбрать один маршрут, например, 1 - 2 - 3 - 1. В третьем случае можно выбрать один маршрут 1 - 2 - 1.
| Название |
|---|




