| Hello 2018 |
|---|
| Закончено |
Вы генерируете вещественные числа s1, s2, ..., sn следующим образом:
- s0 = 0;
- si = si - 1 + ti, где ti — вещественное число, выбранное независимо случайно из равномерного распределения от 0 до 1, включительно.
Даны вещественные числа x1, x2, ..., xn. Вас интересует вероятность того, что si ≤ xi верно для всех i одновременно.
Можно показать, что это число может быть выражено как 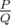 , где P и Q — взаимно простые целые числа, а
, где P и Q — взаимно простые целые числа, а 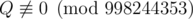 . Выведите значение P·Q - 1 по модулю 998244353.
. Выведите значение P·Q - 1 по модулю 998244353.
Первая строка содержит целое число n (1 ≤ n ≤ 30).
Следующие n строк содержат вещественные числа x1, x2, ..., xn, заданные не более чем с шестью знаками после точки (0 < xi ≤ n).
Выведите одно целое число — ответ на задачу.
4
1.00
2
3.000000
4.0
1
1
0.50216
342677322
2
0.5
1.0
623902721
6
0.77
1.234567
2.1
1.890
2.9999
3.77
859831967
В первом примере искомая вероятность равна 1, так как сумма i вещественных чисел, не превышающих 1, не превышает i.
Во втором примере вероятность равна x1.
В третьем примере искомая вероятность равна 3 / 8.
| Название |
|---|




