Назовем массив a размера n простым, если gcd(a1, a2, ..., an) = 1, где gcd — наибольший общий делитель всех аргументов.
Заданы два числа n и k. Для каждого i (1 ≤ i ≤ k) вам необходимо посчитать количество простых массивов a размера n таких, что для каждого j (1 ≤ j ≤ n) 1 ≤ aj ≤ i. Так как ответы могут быть очень большими, возьмите каждый из них по модулю 109 + 7.
В первой строке записаны два целых числа n и k (1 ≤ n, k ≤ 2·106) — требуемый размер массивов и верхняя граница значений элементов, соответственно.
Вывод 2·106 чисел может занять довольно долгое время, поэтому выведите ответ следующим образом:
Пусть bi — количество простых массивов с элементами в отрезке [1, i], взятое по модулю 109 + 7. Выведите значение 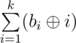 , взятое по модулю 109 + 7. Здесь
, взятое по модулю 109 + 7. Здесь  означает побитовое исключающее ИЛИ (^ в C++ или Java, xor в Pascal).
означает побитовое исключающее ИЛИ (^ в C++ или Java, xor в Pascal).
3 4
82
2000000 8
339310063
Пояснение к примеру:
Так как количество простых массивов велико, мы покажем массивы, которые не являются простыми, но содержат только элементы из отрезка [1, i]:
Для i = 1 единственный массив простой. b1 = 1.
Для i = 2 массив [2, 2, 2] не простой. b2 = 7.
Для i = 3 массивы [2, 2, 2] и [3, 3, 3] не простые. b3 = 25.
Для i = 4 массивы [2, 2, 2], [3, 3, 3], [2, 2, 4], [2, 4, 2], [2, 4, 4], [4, 2, 2], [4, 2, 4], [4, 4, 2] и [4, 4, 4] не простые. b4 = 55.
| Название |
|---|




