| Codeforces Round 457 (Div. 2) |
|---|
| Закончено |
Трудно поверить, но Джейми — финальный босс!
У Джейми есть дерево на n вершинах, пронумерованных от 1 до n. Изначально корнем дерева является вершина с номеров 1. Кроме того, на каждой вершине дерева записано число.
Вам необходимо обрабатывать запросы трёх типов:
1 v — Сделать вершину с номером v корнем дерева.
2 u v x — Прибавить x к значению каждой вершины наименьшего по размеру поддерева, содержащего вершины u и v.
3 v — Найти сумму значений вершин в поддереве вершины v.
Поддерево вершины v — это множество вершин, для которых v лежит на кратчайшем пути от этой вершины до корня. Обратите внимание, что поддерево вершины может измениться в результате изменения корня дерева.
Покажите Джейми вашу мощь и выполните все запросы!
В первой строке через пробел заданы два целых числа n и q (1 ≤ n ≤ 105, 1 ≤ q ≤ 105) — количество вершин и количество запросов, которые требуется обработать, соответственно.
Во второй строке через пробел заданы n целых чисел a1, a2, ..., an ( - 108 ≤ ai ≤ 108) — начальные значения вершин.
В следующих n - 1 строках содержатся пары целых чисел ui, vi (1 ≤ ui, vi ≤ n) обозначающие ребро между вершинами ui и vi в дереве.
Следующие q строк содержат описания запросов.
Каждый запрос задан в одном из следующих форматов в зависимости от типа запроса.
1 v (1 ≤ v ≤ n) для запросов первого типа.
2 u v x (1 ≤ u, v ≤ n, - 108 ≤ x ≤ 108) для запросов второго типа.
3 v (1 ≤ v ≤ n) для запросов третьего типа.
Все числа в описании запросов целые.
Запросы необходимо обрабатывать в заданном порядке. Гарантируется, что заданный граф является деревом.
Для каждого запроса третьего типа выведите ответ на него. Гарантируется, что в тесте есть хотя бы один запрос третьего типа.
6 7
1 4 2 8 5 7
1 2
3 1
4 3
4 5
3 6
3 1
2 4 6 3
3 4
1 6
2 2 4 -5
1 4
3 3
27
19
5
4 6
4 3 5 6
1 2
2 3
3 4
3 1
1 3
2 2 4 3
1 1
2 2 4 -3
3 1
18
21
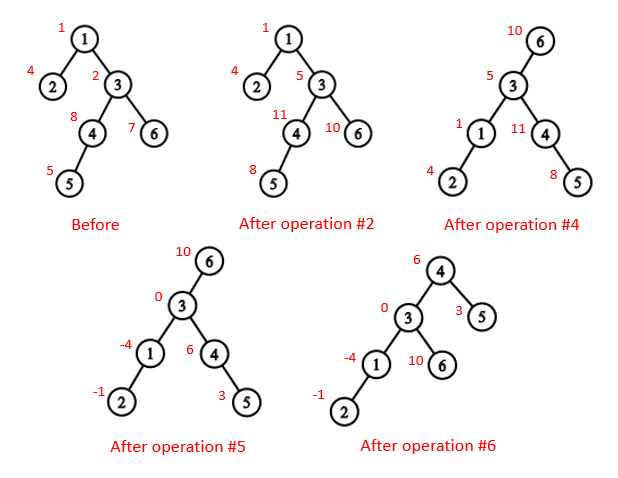
Картинка ниже иллюстрирует изменения дерева в первом тестовом примере.
| Название |
|---|




