Рассмотрим следующую игру для двух игроков. Есть одна белая фишка и ненулевое количество черных фишек. Каждая фишка расположена на координатной плоскости в точке с целыми координатами x и y.
Игроки по очереди, начиная с белых, передвигают все фишки своего цвета на 1 вверх, вниз, влево или вправо. Черные могут выбирать направление для каждой фишки независимо.
После хода белых белая фишка не может находиться в одной точке с черной фишкой. Других ограничений на расположение фишек нет: нескольким черным фишкам разрешено располагаться в одной точке, после хода черных и изначально белая фишка может находится в одной точке с черной. Если в какой-то момент у белых нет хода, то выиграли черные. Если белые сделали хотя бы 10100500 ходов, то они выиграли.
Вам нужно решить следующую задачу. Даны начальные положения всех черных фишек. Гарантируется, что в начале игры все эти положения различны. В скольких местах может находиться белая фишка, чтобы при оптимальной игре выигрывали черные?
Первая строка содержит одно целое число n (1 ≤ n ≤ 105) — количество черных фишек.
В (i + 1)-й строке находятся два целых числа xi, yi ( - 105 ≤ xi, yi, ≤ 105) — координаты точки, в которой стоит i-я черная фишка изначально.
Гарантируется, что все начальные позиции черных фишек различны.
Выведите количество точек, в которых может стоять белая фишка в начале игры, чтобы при оптимальной игре обоих игроков выигрывали черные.
4
-2 -1
0 1
0 -3
2 -1
4
4
-2 0
-1 1
0 -2
1 -1
2
16
2 1
1 2
-1 1
0 1
0 0
1 1
2 -1
2 0
1 0
-1 -1
1 -1
2 2
0 -1
-1 0
0 2
-1 2
4
В первом и втором тесте черными кругами обозначены положения черных фишек, белыми кругами — возможные положения белых фишек, при которых выигрывают черные.
Первый тест: 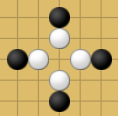
Второй тест: 
В третьем тесте белые фишки должны располагаться во внутреннем квадрате 2 × 2, чтобы выиграли черные. 
| Название |
|---|




