| Codeforces Round 462 (Div. 1) |
|---|
| Закончено |
В гостях хорошо, а дома лучше. Именно поэтому встреча Китайского Нового года всей семьей — такая важная и обязательная традиция.
После праздничного ужина Маленький Томми предложил семье сложную логическую игру. Вот ее краткие правила:
- Изначально перед вами последовательность из n неотрицательных целых чисел p1, p2, ..., pn. По правилам все числа в этой последовательности должны оставаться неотрицательными на протяжении всей игры.
- Вы можете выбрать два соседних положительных целых числа в этой последовательности pi и pi + 1 (1 ≤ i < n) и затем уменьшить их на минимум среди них (т. е. min(pi, pi + 1)), стоимость операции равна величине уменьшения, т. е. min(pi, pi + 1). Назовем такую операцию понижением.
- Игра оканчивается, как только не останется ни одной пары соседних положительных чисел. Ваша задача — довести игру до конца за минимальную суммарную стоимость операций.
Легко видеть, что игра закончится не более чем за n - 1 понижений. Выведите свое решение этой головоломки с минимальной стоимостью.
Первая строка содержит одно целое число n (1 ≤ n ≤ 3·105).
Вторая строка содержит n целых чисел p1, p2, ..., pn (0 ≤ pi ≤ 109, i = 1, 2, ..., n).
В первой строке выведите одно целое число — число понижений в вашем решении m (0 ≤ m ≤ n - 1).
В следующие m строк выведите понижения по порядку. В каждой из этих m строк выведите одно целое число i (1 ≤ i < n), показывающее, что вы будете производить понижение чисел pi и pi + 1.
Если существует несколько решений, минимизирующих стоимость, выведите любое из них.
4
2 1 3 1
2
1
3
5
2 2 1 3 1
3
2
1
4
В первом примере одно из оптимальных решений следующее: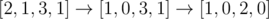 
, итоговая стоимость 1 + 1 = 2.
Во втором примере одно из оптимальных решений следующее: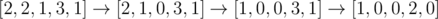 
, итоговая стоимость 1 + 1 + 1 = 3.
