У вас есть полное бинарное дерево с бесконечным количеством уровней.
В каждой вершине записано значение. Если в вершине записано значение x, то в ее левом потомке записано значение 2·x, а в правом потомке — значение 2·x + 1.
Значение, записанное в корне, равно 1.
Вам нужно обработать Q запросов.
Всего есть 3 типа запросов:
- Циклически сдвинуть на K значения, записанные во всех вершинах, которые находятся на одном уровне с вершиной, в которой записано значение X. (Вершины и значения, записанные в вершинах, на других уровнях остаются без изменений).
- Циклически сдвинуть на K вершины, которые находятся на одном уровне с вершиной, в которой записано значение X. (Поддеревья сдвигаемых вершин двигаются вместе с ними).
- Вывести значения, записанные в каждой из вершин, которые встречаются на простом пути из вершины, в которой записано значение X, до корня.
Положительное K означает циклический сдвиг вправо, а отрицательное K означает циклический сдвиг влево.
Гарантируется, что среди запросов есть хотя бы один, который имеет тип 3.
В первой строке следует целое число Q (1 ≤ Q ≤ 105).
Далее следуют Q запросов по одному в строке:
- Запросы типа 1 и 2 имеют следующий формат: T X K (1 ≤ T ≤ 2; 1 ≤ X ≤ 1018; 0 ≤ |K| ≤ 1018), где T обозначает тип запроса.
- Запросы типа 3 имеют следующий формат: 3 X (1 ≤ X ≤ 1018).
Для каждого запроса типа 3 выведите в порядке убывания значения, записанные во всех вершинах, встречающихся на пути.
5
3 12
1 2 1
3 12
2 4 -1
3 8
12 6 3 1
12 6 2 1
8 4 2 1
5
3 14
1 5 -3
3 14
1 3 1
3 14
14 7 3 1
14 6 3 1
14 6 2 1
На картинках ниже изображены первые 4 уровня дерева для первого примера:
Изначальное дерево:
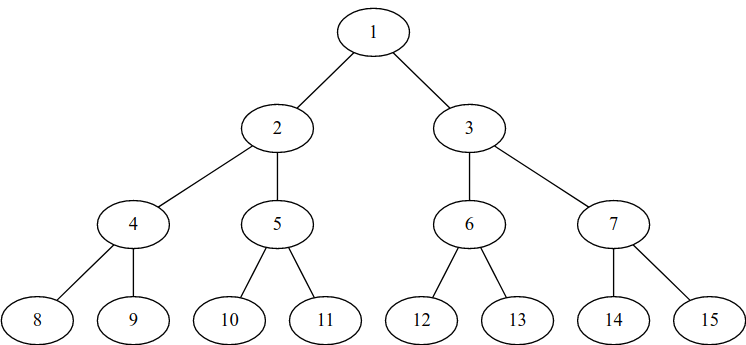
Дерево после запроса 1 2 1:
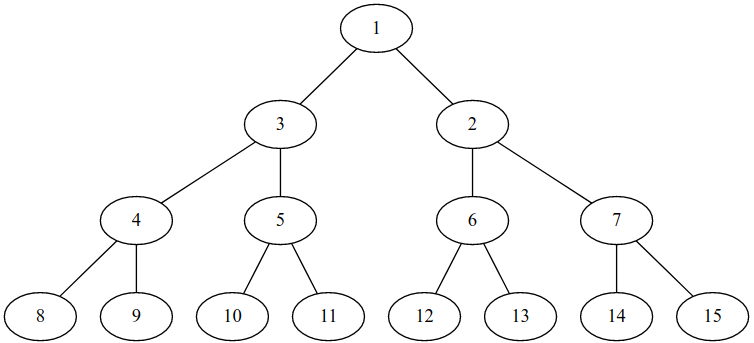
Дерево после запроса 2 4 -1:
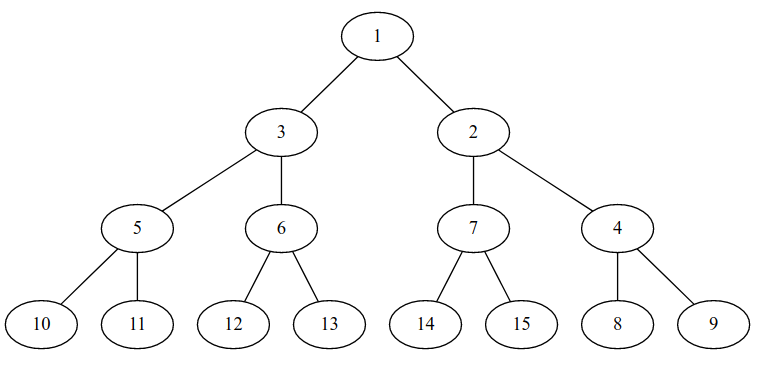
| Название |
|---|




