Вам дан ориентированный граф с n вершинами и m рёбер, каждое из которых имеет определённый вес.
В нём могут быть кратные рёбра и петли, кроме того, граф может быть несвязным.
Вам нужно выбрать путь (возможно, проходящий по одному и тому же ребру или вершине несколько раз) такой, что веса рёбер в пути находятся в строго возрастающем порядке, а кроме того, все ребра пути идут в том же порядке, в котором они находились во входных данных. Найдите максимально возможное количество ребер в таком пути.
Обратите внимание, ребра пути не обязательно должны идти последовательно во входных данных.
В первой строке содержатся два целых числа n и m (1 ≤ n ≤ 100000,1 ≤ m ≤ 100000) — число вершин и рёбер в графе соответственно.
После этого следует m строк, в i-й из которых содержится три целых числа, разделённых пробелами — ai, bi и wi (1 ≤ ai, bi ≤ n, 0 ≤ wi ≤ 100000), обозначающих, что есть ребро от вершины ai до вершины bi с весом wi.
Выведите одно целое число в одной строке — максимальное количество рёбер в пути.
3 3
3 1 3
1 2 1
2 3 2
2
5 5
1 3 2
3 2 3
3 4 5
5 4 0
4 5 8
3
Ответ на первый пример — 2: 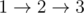 .
.
Заметим, что нельзя выбрать путь  , потому что ребро
, потому что ребро 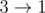 появляется в вводе раньше, чем два других ребра, и поэтому его нельзя выбрать после того, как было выбрано какое-то из двух других рёбер.
появляется в вводе раньше, чем два других ребра, и поэтому его нельзя выбрать после того, как было выбрано какое-то из двух других рёбер.
Во втором примере оптимально выбрать 1-е, 3-е и 5-е ребра, чтобы получить оптимальный ответ:  .
.
| Название |
|---|




