→ Виртуальное участие
Виртуальное соревнование – это способ прорешать прошедшее соревнование в режиме, максимально близком к участию во время его проведения. Поддерживается только ICPC режим для виртуальных соревнований.
Если вы раньше видели эти задачи,
виртуальное соревнование не для вас – решайте эти задачи в архиве.
Если вы хотите просто дорешать задачи, виртуальное соревнование не для вас – решайте эти задачи в архиве.
Запрещается использовать чужой код, читать разборы задач и общаться по содержанию соревнования с кем-либо.
→ Теги задачи
геометрия
*2000
Нет прав на редактирование
→ Материалы соревнования
Условие задачи было недавно изменено. Просмотреть изменения.
×
D. Пара прямых
ограничение по времени на тест
2 секундыограничение по памяти на тест
256 мегабайтввод
стандартный вводвывод
стандартный выводЗадано n точек на плоскости, все точки имеют целочисленные координаты. Все точки различны.
Необходимо узнать, существуют ли две такие прямые, что каждая из заданных точек принадлежит хотя бы одной из них. Прямые могут совпадать.
Входные данные
В первой строке задано одно целое число n (1 ≤ n ≤ 105) — количество точек на плоскости.
Далее в n строках заданы по два целых числа xi и yi (|xi|, |yi| ≤ 109)— координаты i-й точки. Все n точек различны.
Выходные данные
Если возможно провести две прямые так, что каждая точка лежит хотя бы на одной из них, то выведите YES, иначе NO.
Примеры
Входные данные
5
0 0
0 1
1 1
1 -1
2 2
Выходные данные
YES
Входные данные
5
0 0
1 0
2 1
1 1
2 3
Выходные данные
NO
Примечание
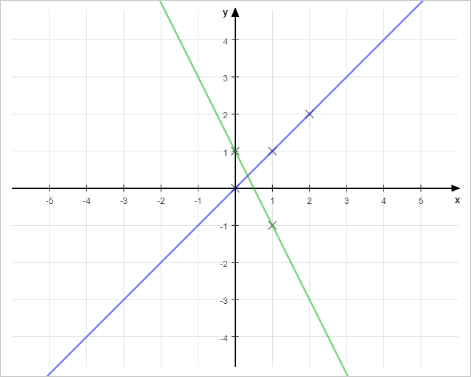
В первом примере можно провести две прямые так, что первая проходит через точки под номерами 1, 3 и 5, а вторая — через две оставшиеся точки.
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 20.11.2024 14:31:00 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




