→ Виртуальное участие
Виртуальное соревнование – это способ прорешать прошедшее соревнование в режиме, максимально близком к участию во время его проведения. Поддерживается только ICPC режим для виртуальных соревнований.
Если вы раньше видели эти задачи,
виртуальное соревнование не для вас – решайте эти задачи в архиве.
Если вы хотите просто дорешать задачи, виртуальное соревнование не для вас – решайте эти задачи в архиве.
Запрещается использовать чужой код, читать разборы задач и общаться по содержанию соревнования с кем-либо.
→ Теги задачи
бинарный поиск
строковые суфф. структуры
хэши
*2700
Нет прав на редактирование
→ Материалы соревнования
Условие задачи было недавно изменено. Просмотреть изменения.
×
F. K-подстроки
ограничение по времени на тест
4 секундыограничение по памяти на тест
256 мегабайтввод
стандартный вводвывод
стандартный выводДана строка s, состоящая из n строчных латинских букв.
Назовем k-подстрокой строки s строку subsk = sksk + 1..sn + 1 - k. очевидно, что subs1 = s и существует ровно 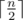 таких подстрок.
таких подстрок.
Назовём нечётным собственным супрефиксом строки T такую строку t, что выполняются следующие условия:
- |T| > |t|;
- |t| нечётно;
- t является одновременно и префиксом, и суффиксом T.
Для каждой k-подстроки (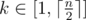 ) s найдите наибольшую длину нечётного собственного супрефикса этой строки.
) s найдите наибольшую длину нечётного собственного супрефикса этой строки.
Входные данные
В первой строке задано натуральное число n (2 ≤ n ≤ 106) — длина строки s.
Во второй строке задана строка s, состоящая из n строчных букв латинского алфавита.
Выходные данные
Выведите 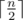 целых чисел, где i-е число равно наибольшей длине нечётного собственного супрефикса i-подстроки s (или - 1, если у i-подстроки нет нечётных собственных супрефиксов).
целых чисел, где i-е число равно наибольшей длине нечётного собственного супрефикса i-подстроки s (или - 1, если у i-подстроки нет нечётных собственных супрефиксов).
Примеры
Входные данные
15
bcabcabcabcabca
Выходные данные
9 7 5 3 1 -1 -1 -1
Входные данные
24
abaaabaaaabaaabaaaabaaab
Выходные данные
15 13 11 9 7 5 3 1 1 -1 -1 1
Входные данные
19
cabcabbcabcabbcabca
Выходные данные
5 3 1 -1 -1 1 1 -1 -1 -1
Примечание
Ответ на первый пример следующий:
- 1-подстрока: bcabcabcabcabca
- 2-подстрока: cabcabcabcabc
- 3-подстрока: abcabcabcab
- 4-подстрока: bcabcabca
- 5-подстрока: cabcabc
- 6-подстрока: abcab
- 7-подстрока: bca
- 8-подстрока: c
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 20.11.2024 14:34:34 (g1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




