Дано множество из n элементов, пронумерованных от 1 до n. Вес i-го объекта равен wi. Вес некоторого подмножества этого множества рассчитывается по формуле 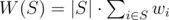 . Вес разбиения R данного множества на k подмножеств равен
. Вес разбиения R данного множества на k подмножеств равен 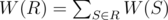 (напоминаем, разбиением называется множество таких подмножеств данного множества, что каждый элемент данного множества принадлежит ровно одному множеству из разбиения).
(напоминаем, разбиением называется множество таких подмножеств данного множества, что каждый элемент данного множества принадлежит ровно одному множеству из разбиения).
Посчитайте суммарный вес всех различных разбиений данного множества на k непустых подмножеств по модулю 109 + 7. Два разбиения считаются различными, если существуют два объекта x и y, такие, что в одном разбиении они принадлежат разным множествам, а в другом — одному и тому же.
В первой строке заданы целые числа n и k (1 ≤ k ≤ n ≤ 2·105) — количество элементов в множестве и количество подмножеств в разбиении.
Во второй строке задано через пробел n целых чисел wi (1 ≤ wi ≤ 109)— соответствующие веса элементов.
Выведите единственное число — суммарный вес всех различных разбиений на k непустых подмножеств по модулю 109 + 7.
4 2
2 3 2 3
160
5 2
1 2 3 4 5
645
Возможные разбиения в первом тесте из условия:
- {{1, 2, 3}, {4}}, W(R) = 3·(w1 + w2 + w3) + 1·w4 = 24;
- {{1, 2, 4}, {3}}, W(R) = 26;
- {{1, 3, 4}, {2}}, W(R) = 24;
- {{1, 2}, {3, 4}}, W(R) = 2·(w1 + w2) + 2·(w3 + w4) = 20;
- {{1, 3}, {2, 4}}, W(R) = 20;
- {{1, 4}, {2, 3}}, W(R) = 20;
- {{1}, {2, 3, 4}}, W(R) = 26;
Возможные разбиения в втором тесте из условия:
- {{1, 2, 3, 4}, {5}}, W(R) = 45;
- {{1, 2, 3, 5}, {4}}, W(R) = 48;
- {{1, 2, 4, 5}, {3}}, W(R) = 51;
- {{1, 3, 4, 5}, {2}}, W(R) = 54;
- {{2, 3, 4, 5}, {1}}, W(R) = 57;
- {{1, 2, 3}, {4, 5}}, W(R) = 36;
- {{1, 2, 4}, {3, 5}}, W(R) = 37;
- {{1, 2, 5}, {3, 4}}, W(R) = 38;
- {{1, 3, 4}, {2, 5}}, W(R) = 38;
- {{1, 3, 5}, {2, 4}}, W(R) = 39;
- {{1, 4, 5}, {2, 3}}, W(R) = 40;
- {{2, 3, 4}, {1, 5}}, W(R) = 39;
- {{2, 3, 5}, {1, 4}}, W(R) = 40;
- {{2, 4, 5}, {1, 3}}, W(R) = 41;
- {{3, 4, 5}, {1, 2}}, W(R) = 42.
| Название |
|---|




