| Яндекс.Алгоритм 2011: Финал |
|---|
| Закончено |
В одном университете совсем недавно узнали о существовании соревнования по спортивному программированию под названием ACM ICPC v2.0. Данное соревнование мало чем отличается от всем известного ACM ICPC, например, в финале соревнования участникам запрещается участвовать более двух раз. Однако, есть одно существенное отличие: команды в этом состязании должны состоять ровно из n участников.
Поучаствовав в нескольких финалах ACM ICPC v2.0 и не добившись ни одной медали, студенты и руководство университета поняли, что настало время изменить что-то в процессе подготовки. В частности, в качестве первой инновации было решено изменить процесс формирования команд. Потратив немалое количество времени на изучение статистики выступлений других университетов, удалось получить некоторую интересную информацию: вероятность получения медали в зависимости от количества членов команды, побывавших на финале ранее. Более формально, известно n + 1 действительных чисел p0 ≤ p1 ≤ ... ≤ pn, где pi — вероятность получения медали на финале, если в команде присутствуют i участников прошлых финалов, а остальные n - i участников приехали на финал впервые.
Несмотря на такие полезные данные, руководство университета не в состоянии определить такую тактику формирования команд, которая обеспечит максимальную вероятность получения медали на финале ACM ICPC v2.0 в среднем (подразумевается, что мы хотим обеспечить такой результат на далекое будущее и обладаем бесконечным ресурсом студентов). А сможете ли вы предложить такую оптимальную тактику? На первом этапе руководству университета достаточно знать лишь значение максимальной средней вероятности.
Более формально: пусть в k-ый год участия университет послал на финал команду, в которой было ak участников финалов прошлых лет (0 ≤ ak ≤ n). Так как один человек может участвовать в финале не более двух раз, должно выполняться условие: 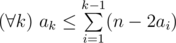 . Ваша задача — выбрать последовательность
. Ваша задача — выбрать последовательность 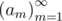 таким образом, что предел Ψ существует и его значение максимально:
таким образом, что предел Ψ существует и его значение максимально:
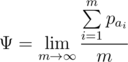
Так как 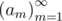 — бесконечная последовательность, вывести требуется только максимальное значение предела Ψ.
— бесконечная последовательность, вывести требуется только максимальное значение предела Ψ.
В первой строке задано целое число n (3 ≤ n ≤ 100), n — количество участников команды. Во второй строке заданы n + 1 действительных чисел, с не более чем 6-ю знаками после десятичной точки, pi (0 ≤ i ≤ n, 0 ≤ pi ≤ 1) — вероятность того, что команда сможет выиграть медаль, если в ее состав входят i участников, побывавших на финале ранее. Также выполняется условие, что pi ≤ pi + 1 для всех 0 ≤ i ≤ n - 1.
Выведите одно единственное действительное число — ожидаемое среднее количество выигранных медалей в год, при использовании оптимальной стратегии. Для ответа допустима абсолютная или относительная погрешность 10 - 6.
3
0.115590 0.384031 0.443128 0.562356
0.4286122500
3
1 1 1 1
0.9999999999
Во втором тесте, из каких бы участников не состояла команда, она обречена на успех.
| Название |
|---|




