Задан двудольный неориентированный граф G = (U, V, E), U — множество вершин в первой доле, V — множество вершин во второй доле, E — множество ребер. Могут встречаться кратные ребра.
Назовем некоторое подмножество его ребер 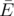 k-покрытием тогда и только тогда, когда в графе
k-покрытием тогда и только тогда, когда в графе 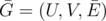 каждой вершине инциндентно не менее k ребер. Минимальным k-покрытием называется такое k-покрытие, что размер множества
каждой вершине инциндентно не менее k ребер. Минимальным k-покрытием называется такое k-покрытие, что размер множества 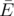 минимален.
минимален.
Ваша задача — найти минимальное k-покрытие для каждого 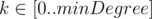 , где minDegree — это минимальная степень какой-либо вершины в графе G.
, где minDegree — это минимальная степень какой-либо вершины в графе G.
В первой строке записаны три целых числа n1, n2 и m (1 ≤ n1, n2 ≤ 2000, 0 ≤ m ≤ 2000) — количество вершин в первой доле, количество вершин во второй доле и количество ребер, соответственно.
В i-й из следующих m строк записаны два целых числа ui и vi (1 ≤ ui ≤ n1, 1 ≤ vi ≤ n2) — описание i-го ребра, ui — номер вершины в первой доле и vi — номер вершины во второй доле.
Для каждого 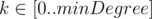 выведите подмножество ребер (минимальное k-покрытие) в отдельной строке.
выведите подмножество ребер (минимальное k-покрытие) в отдельной строке.
Первое число cntk в k-й строке — это количество ребер в минимальном k-покрытии графа. Затем идут cntk целых чисел — оригинальные номера ребер, которые принадлежат минимальному k-покрытию, эти номера должны быть попарно различны. Ребра пронумерованы от 1 до m в таком же порядке, в котором встречаются во входных данных.
3 3 7
1 2
2 3
1 3
3 2
3 3
2 1
2 1
0
3 3 7 4
6 1 3 6 7 4 5
1 1 5
1 1
1 1
1 1
1 1
1 1
0
1 5
2 4 5
3 3 4 5
4 2 3 4 5
5 1 2 3 4 5
| Название |
|---|




