| Codeforces Round 479 (Div. 3) |
|---|
| Закончено |
Вам задан неориентированный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер. Ваша задача — найти количество компонент связности, которые являются циклами.
Вот несколько определений из теории графов.
Неориентированный граф состоит из двух множеств: множества узлов (называемых вершинами) и множества рёбер. Каждое ребро соединяет пару вершин. Все ребра двунаправленные (то есть если вершина $$$a$$$ соединена с вершиной $$$b$$$, вершина $$$b$$$ тоже соединена с вершиной $$$a$$$). Ребро не может соединять вершину саму с собой, также не может существовать более одного ребра между парой вершин.
Две вершины $$$u$$$ и $$$v$$$ принадлежат одной компоненте связности тогда и только тогда, когда существует хотя бы один путь по ребрам, соединяющий $$$u$$$ и $$$v$$$.
Компонента связности является циклом тогда и только тогда, когда все ее вершины могут быть переупорядочены следующим образом:
- первая вершина соединена ребром со второй вершиной,
- вторая вершина соединена ребром с третьей вершиной,
- ...
- последняя вершина соединена ребром с первой вершиной,
- все описанные выше ребра цикла — различны.
Цикл содержит только вершины и ребра, описанные выше. По определению цикл содержит не менее трех вершин.
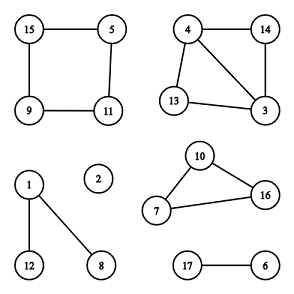Граф на рисунке содержит $$$6$$$ компонент связности, $$$2$$$ из них являются циклами: $$$[7, 10, 16]$$$ и $$$[5, 11, 9, 15]$$$. В первой строке входных данных задано два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le m \le 2 \cdot 10^5$$$) — количество вершин и рёбер в графе.
В следующих $$$m$$$ строках заданы рёбра: $$$i$$$-е ребро задаётся парой вершин $$$v_i$$$, $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$u_i \ne v_i$$$). Гарантируется, что граф не содержит кратных рёбер (то есть для любой пары ($$$v_i, u_i$$$) не существует других пар ($$$v_i, u_i$$$) и ($$$u_i, v_i$$$) среди заданных рёбер).
Выведите одно целое число — количество компонент связности, которые являются циклами.
5 4
1 2
3 4
5 4
3 5
1
17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6
2
В первом тестовом примере только компонента $$$[3, 4, 5]$$$ является циклом.
Второй пример соответствует рисунку из условия.
