У Аркадия есть бесконечная плоскость, изначально покрашенная в цвет номер $$$0$$$. Затем он по очереди рисует на плоскости $$$n$$$ закрашенных прямоугольников со сторонами, параллельными декартовым осям координат. Цвет $$$i$$$-го прямоугольника равен $$$i$$$ (прямоугольники пронумерованы от $$$1$$$ до $$$n$$$ в порядке покраски). Возможно, что новые прямоугольники закрашивают некоторые предыдущие целиком или частично.
Посчитайте, сколько различных цветов будет на рисунке после того, как Аркадий нарисует все прямоугольники.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 100\,000$$$) — количество прямоугольников.
В $$$i$$$-й из следующих $$$n$$$ строк содержится $$$4$$$ целых числа $$$x_1$$$ $$$y_1$$$ $$$x_2$$$ $$$y_2$$$ ($$$-10^9 \le x_1 < x_2 \le 10^9$$$, $$$-10^9 \le y_1 < y_2 \le 10^9$$$) — координаты углов $$$i$$$-го прямоугольника.
В единственной строке выведите единственное число — количество видимых цветов, включая цвет $$$0$$$.
5
-1 -1 1 1
-4 0 0 4
0 0 4 4
-4 -4 0 0
0 -4 4 0
5
4
0 0 4 4
-4 -4 0 0
0 -4 4 0
-2 -4 2 4
5
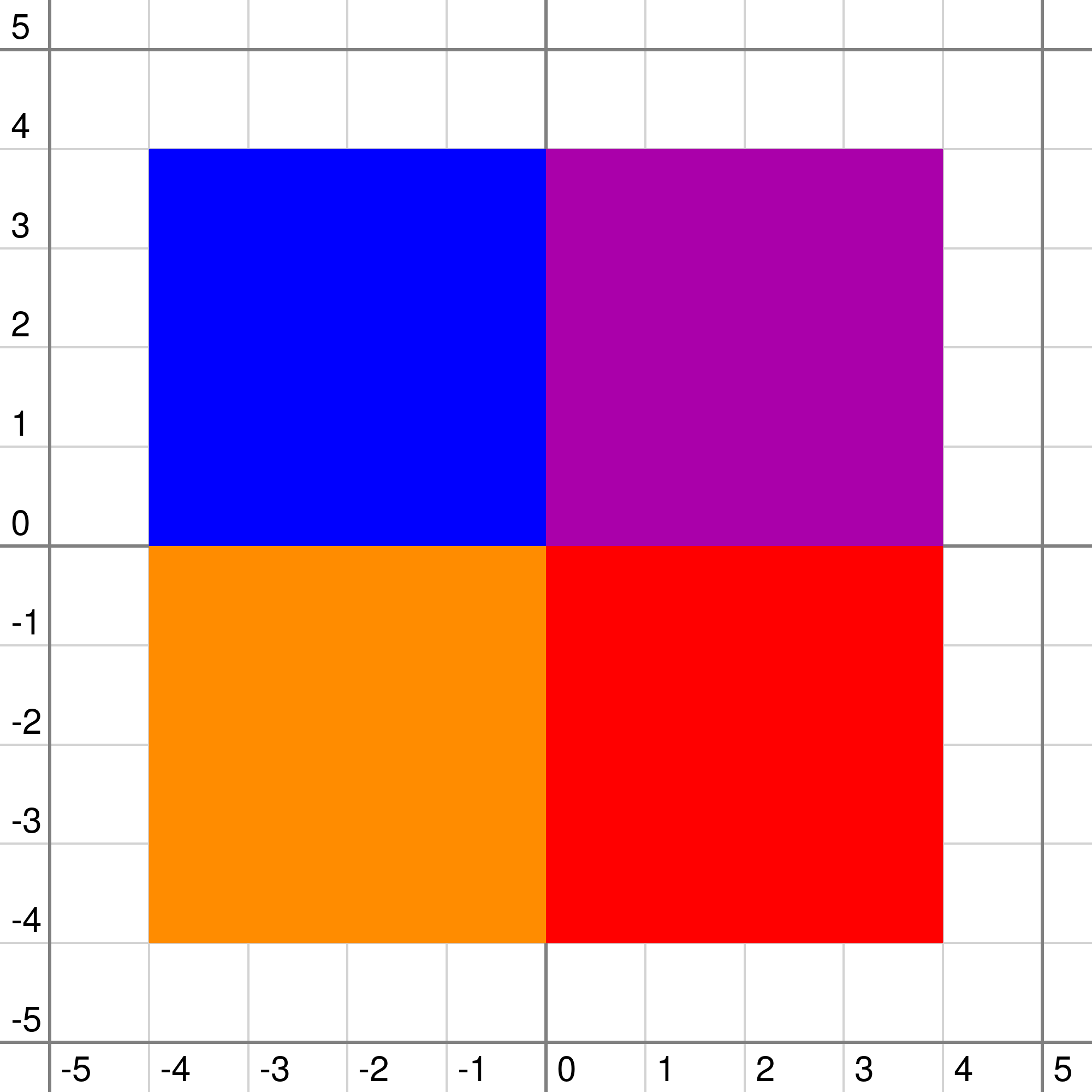Так выглядит плоскость в первом примере.
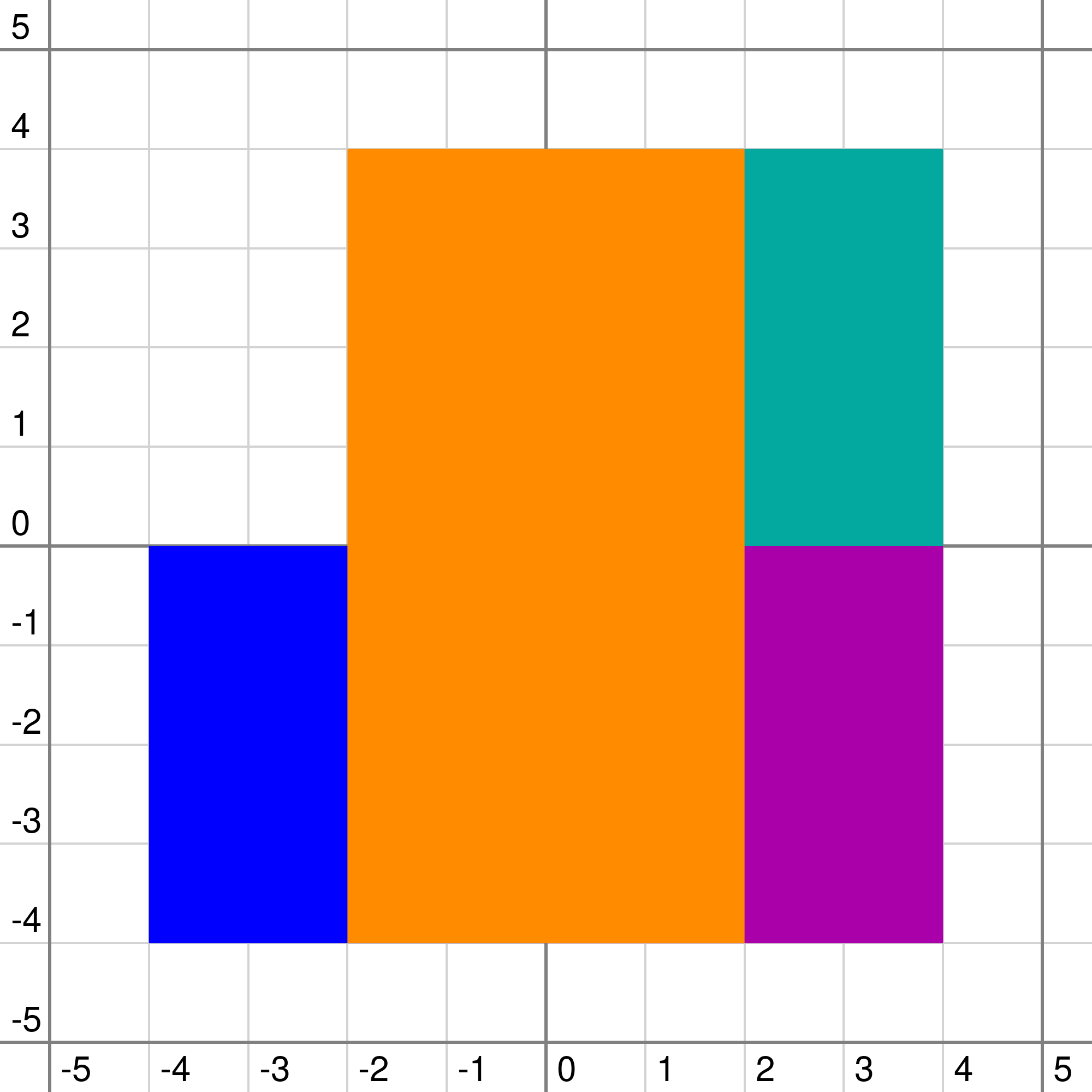Так выглядит плоскость во втором примере.
$$$0$$$ = белый, $$$1$$$ = циановый, $$$2$$$ = синий, $$$3$$$ = фиолетовый, $$$4$$$ = жёлтый, $$$5$$$ = красный.
