Вам дана строка s длины n, состоящая из строчных букв латинского алфавита.
Для двух заданных строк s и t назовем S — множество всех различных букв строки s и T множество всех различных букв строки t. Строки s и t называются изоморфными если их длины равны и существует взаимо-однозначное соответствие (биекция) f между S и T для которого f(si) = ti. Формально:
- f(si) = ti для всех индексов i,
- для любого символа
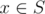существует ровно один символ 
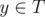, что f(x) = y, - для любого символа 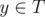существует ровно один символ 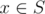, что f(x) = y,.
Например, строки «aababc» b «bbcbcz» изоморфные. Аналогично, строки «aaaww» и «wwwaa» изоморфные. Но следующие пары строк неизоморфны: «aab» и «bbb», «test» и «best».
Обработайте m запросов, каждый состоит из трех целых чисел x, y, len (1 ≤ x, y ≤ n - len + 1). Для каждого запроса проверьте, правда ли две подстроки s[x... x + len - 1] и s[y... y + len - 1] изоморфны.
В первой строке через пробел заданы целые числа n и m (1 ≤ n ≤ 2·105, 1 ≤ m ≤ 2·105) — длина строки s и количество запросов.
Вторая строка содержит s — n строчных букв латинского алфавита.
Следующие m строк содержат описания запросов: xi, yi и leni (1 ≤ xi, yi ≤ n, 1 ≤ leni ≤ n - max(xi, yi) + 1) — параметры очередного запроса.
Для каждого запроса на отдельной строке выведите «YES», если подстроки s[xi... xi + leni - 1] и s[yi... yi + leni - 1] изоморфны, и «NO» в противном случае.
7 4
abacaba
1 1 1
1 4 2
2 1 3
2 4 3
YES
YES
NO
YES
Запросы в примере следующие:
- подстроки «a» и «a» изоморфны: f(a) = a;
- подстроки «ab» и «ca» изоморфны: f(a) = c, f(b) = a;
- подстроки «bac» и «aba» неизоморфны, так как f(b) и f(c) должны быть равны a одновременно;
- подстроки «bac» и «cab» изоморфны: f(b) = c, f(a) = a, f(c) = b.
