Аллен мечтает, что когда-нибудь у него будет большой парк электрокаров — машин будущего. Как только Аллен задумался о том, какие у него будут машины и как он будет их расставлять, он столкнулся с проблемой.
Будущая парковка Аллена может быть представлена как таблица из $$$4$$$ строк и $$$n$$$ ($$$n \le 50$$$) столбцов, каждая клетка которой может вместить в любой момент времени ровно одну машину. У Аллена будет $$$k$$$ ($$$k \le 2n$$$) машин на парковке, все машины изначально расположены во второй и третьей строках. У каждой машины есть предназначенное для нее место в первом или четвертом ряду. Аллену нужно переместить каждую машину на соответствующее ей парковочное место.
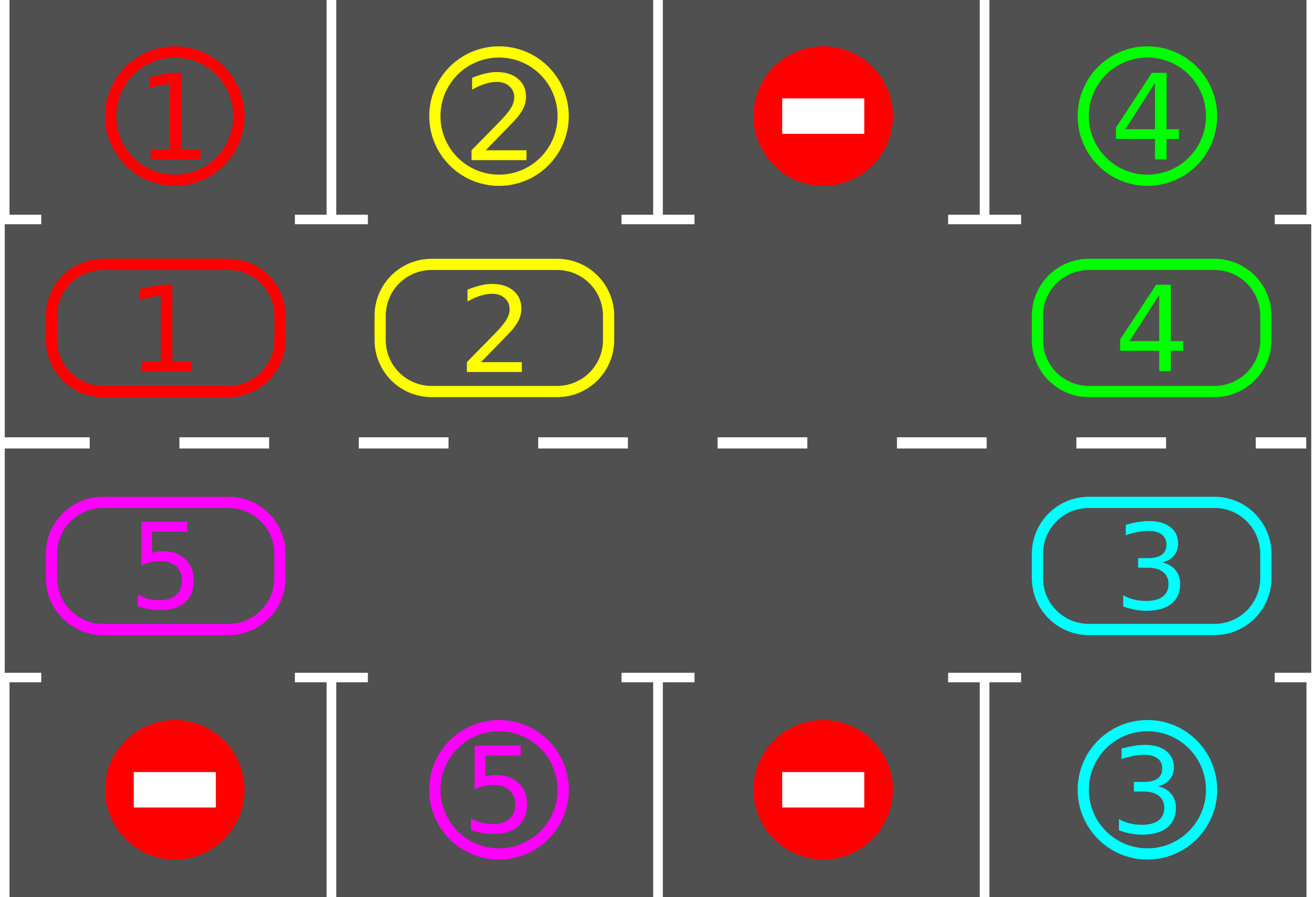Иллюстрация к первому примеру. Сложность состоит в том, что Аллен не может никому доверить машины, поэтому одновременно может двигаться только одна машина. За один шаг он может переместить любую машину в любом из четырех направлений на соседнее пустое место. Однако, машину можно передвигать в первый и четвертый ряд, только если это — соответствующее машине парковочное место.
Аллен будет очень занятым, поэтому у него будет время только на $$$20000$$$ передвижений машин. Помогите Аллену найти способ расставить машины на соответствующие парковочные места, или определите, что это невозможно.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n \le 50$$$, $$$1 \le k \le 2n$$$), обозначающие число столбцов в таблице и число машин, соответственно.
Следующие четыре строки содержат по $$$n$$$ целых чисел, каждов от $$$0$$$ до $$$k$$$ включительно, они описывают начальное состояние парковки. Строки пронумерованы от $$$1$$$ до $$$4$$$ сверху вниз, а столбцы пронумерованы от $$$1$$$ до $$$n$$$ слева направо.
В первой и последней строке целое число $$$1 \le x \le k$$$ обозначает парковочное место машины $$$x$$$ (сюда может заезжать только эта машина), а число $$$0$$$ означает пустое место (сюда не может заехать ни одна машина).
Во второй и третьей строках целое число $$$1 \le x \le k$$$ обозначает начальную позицию машины $$$x$$$, а число $$$0$$$ обозначает пустое место (на него могут заезжать все машины).
Каждое число $$$x$$$ между $$$1$$$ и $$$k$$$ встречается ровно один раз во второй и третьей строках, и ровно один раз в первой и четвертой строках.
Если есть последовательность передвижений машин такая, что все машины окажутся на своих местах за не более чем $$$20000$$$ шагов, выведите $$$m$$$, число шагов, на первой строке. В следующих $$$m$$$ строках выведите шаги по одному в строке в формате $$$i$$$ $$$r$$$ $$$c$$$, что означает, что Аллен должен подвинуть машину $$$i$$$ на соседнее место в строке $$$r$$$ и столбце $$$c$$$.
Если невозможно передвинуть все машины на правильные места за $$$20000$$$ шагов, выведите $$$-1$$$ в единственной строке.
4 5
1 2 0 4
1 2 0 4
5 0 0 3
0 5 0 3
6
1 1 1
2 1 2
4 1 4
3 4 4
5 3 2
5 4 2
1 2
1
2
1
2
-1
1 2
1
1
2
2
2
1 1 1
2 4 1
В первом примере все машины уже располагаются перед соответствующими парковочными местами, кроме машины $$$5$$$, которая находится напротив соседнего места. Пример показывает кратчайшее решение, но будет зачтено любое длины не более $$$20000$$$.
Во втором примере есть только один столбец, и машины находятся в неправильном порядке, поэтому они не могут двигаться и расставить их правильным образом невозможно.
