| Codeforces Round 493 (Div. 1) |
|---|
| Закончено |
Рассмотрим дерево (то есть неориентированный связный граф без циклов) $$$T_1$$$ и дерево $$$T_2$$$. Определим их декартово произведение $$$T_1 \times T_2$$$ следующим образом.
Пусть $$$V$$$ — множество вершин $$$T_1$$$, а $$$U$$$ — множество вершин $$$T_2$$$.
Тогда множеством вершин $$$T_1 \times T_2$$$ является $$$V \times U$$$, то есть множество упорядоченных пар вершин, где первая вершина из $$$V$$$, а вторая из $$$U$$$.
Проведём ребра следующего вида:
- Между $$$(v, u_1)$$$ и $$$(v, u_2)$$$ есть неориентированное ребро, если $$$u_1$$$ и $$$u_2$$$ смежны в графе $$$U$$$.
- Аналогично между $$$(v_1, u)$$$ и $$$(v_2, u)$$$ есть неориентированное ребро, если $$$v_1$$$ и $$$v_2$$$ смежны в графе $$$V$$$.
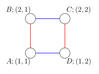
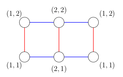
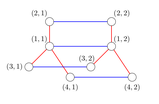
Обратите внимание на пояснения к примерам, они содержат картинки для произведения деревьев для тестов из примеров.
Рассмотрим граф $$$T_1 \times T_2$$$. Вычислите количество циклов в этом графе (не обязательно простых) длины $$$k$$$. Выведите остаток при делении найденного количества на $$$998244353$$$.
Циклом называется последовательность вершин $$$w_1$$$, $$$w_2$$$, ..., $$$w_k$$$, где $$$w_i \in V \times U$$$, такая что любые две соседние вершины смежны, а также $$$w_1$$$ смежно с $$$w_k$$$. Циклы отличающиеся только циклическим сдвигом или направлением обхода всё равно считаются различными.
В первой строке входного файла даны три числа — $$$n_1$$$, $$$n_2$$$ и $$$k$$$ ($$$2 \le n_1, n_2 \le 4000$$$, $$$2 \le k \le 75$$$) — размер первого дерева, второго дерева и длина цикла соответственно.
Затем следует $$$n_1 - 1$$$ строка описывающая первое дерево. Каждая из этих строк содержит два числа — $$$v_i, u_i$$$ ($$$1 \le v_i, u_i \le n_1$$$), задающие соответствующее ребро графа.
Каждая из следующих $$$n_2 - 1$$$ строк задаёт второе дерево в том же формате.
Гарантируется, что заданные графы являются деревьями.
Выведите одно число — количество циклов по модулю $$$998244353$$$.
2 2 2
1 2
1 2
8
2 2 4
1 2
1 2
32
2 3 4
1 2
1 2
1 3
70
4 2 2
1 2
1 3
1 4
1 2
20
Следующие три картинки иллюстрируют графы, которые получаются в результате произведения в тестах из условия.
В первом примере список циклов длины $$$2$$$ следующий:
- «AB», «BA»
- «BC», «CB»
- «AD», «DA»
- «CD», «DC»
| Название |
|---|




